Question

There are exactly two points on the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ whose distance from its centre is same and equal to $\sqrt{\dfrac{{{a}^{2}}+2{{b}^{2}}}{2}}$. Then the eccentricity of the ellipse is:
A. $\dfrac{1}{2}$
B. $\dfrac{1}{\sqrt{2}}$
C. $\dfrac{1}{3}$
D. $\dfrac{1}{3\sqrt{2}}$

Answer 1

Here, in this problem, we need to use the general equation of ellipse which is given that is $\dfrac{{{x}^{2}}}{a}+\dfrac{{{y}^{2}}}{b}=1$ whose distance is same that means the point is on either minor or major axis hence, we consider the $a=\sqrt{\dfrac{{{a}^{2}}+2{{b}^{2}}}{2}}$ by solving and simplifying this and substituting in the formula of eccentric that is $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ then we get the value of eccentric of the ellipse.

Complete step by step answer:
In this problem, it is given that general equation of ellipse that is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and also given the condition is that distance from the center is same and is equal to $\sqrt{\dfrac{{{a}^{2}}+2{{b}^{2}}}{2}}$.
For more understanding of the question figure of ellipse is given below:

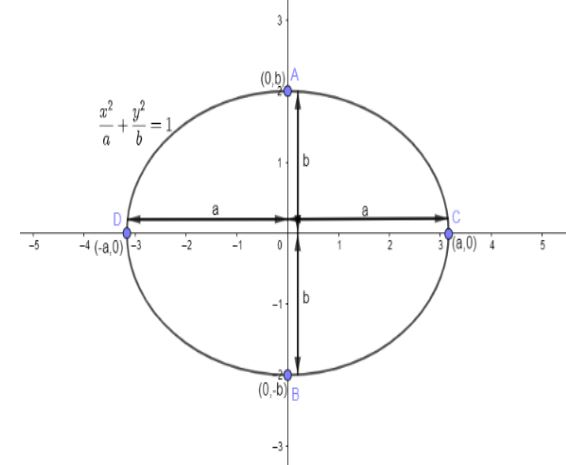
Here, in the figure, ACBD is an ellipse and general equation of ellipse is given that $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Points at C $(a,0)$, D $(-a,0)$, A $(0,b)$ and B $(0,b)$. These are the points given in the figure of the ellipse. According to the conditions in the given question that distance from the center is the same, the points would be either endpoints of the major axis or of the minor axis.But $\sqrt{\dfrac{{{a}^{2}}+2{{b}^{2}}}{2}}>b$ so the points are the vertices of major axis.Hence, it is considered that $a=\sqrt{\dfrac{{{a}^{2}}+2{{b}^{2}}}{2}}$

By squaring on both sides, we get:
${{a}^{2}}=\dfrac{{{a}^{2}}+2{{b}^{2}}}{2}$
By multiplying 2 on both sides, we get:
$2{{a}^{2}}=2\times \dfrac{{{a}^{2}}+2{{b}^{2}}}{2}$
If you notice in RHS then you can see that 2 get cancelled on numerator and denominator we get:
$2{{a}^{2}}={{a}^{2}}+2{{b}^{2}}$
By rearranging the term, we get:
$2{{a}^{2}}-{{a}^{2}}=2{{b}^{2}}$
By solving this we get:
${{a}^{2}}=2{{b}^{2}}--(1)$

Now, to find the eccentric, we know the formula of eccentric which is given by $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}--(2)$
Here, by substituting the value of equation (1) on equation (2) we get:
$e=\sqrt{1-\dfrac{{{b}^{2}}}{2{{b}^{2}}}}$
Here, you can see that ${{b}^{2}}$ get cancelled then we get:
$e=\sqrt{1-\dfrac{1}{2}}$
By cross multiplying on RHS we get:
$e=\sqrt{\dfrac{2-1}{2}}$
By simplifying further, we get:
$e=\sqrt{\dfrac{1}{2}}$
Or it can also be written as $e=\dfrac{1}{\sqrt{2}}$.
Hence, the eccentricity of the ellipse is $\dfrac{1}{\sqrt{2}}$.

So, the correct option is “option B”.

Note: Here, there is another approach to solve after this step that is ${{a}^{2}}=2{{b}^{2}}$. In the given solution we have substituted the value of ${{a}^{2}}$ in the formula of eccentricity. Another approach is that, you can also substitute the value of ${{b}^{2}}$ in the formula of eccentric then we will get in the term of ${{a}^{2}}$ and it’s cancelled then you will get the same answer as in the above solution. Always remember the concept of eccentric that when the equation of ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ then with the major axis along y axis and minor along x axis and its foci will be $(0,ae)$ and $(0,-ae)$. Thus, in general, the ellipse centred at $(h,k)$ can be represented by the formula $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$ or vice versa according to the axis where the ellipse is oriented.