Question

There are 10 units of charge at the centre of a circle of radius 10m. The work done in moving one unit of charge around the circle once is:
A) 0
B) 10 units
C) 100 units
D) 1 unit

Answer 1

To solve this particular question one must have a clear idea about the concept of the relationship between potential difference, charge and work done. It is a known fact that the potential difference between two points or terminals is the work required in Joules to move one Coulomb of charge.

Complete step by step solution:
It is given that the magnitude of charge is 10 units and it lies at the center of a circle whose radius is 10m. Now suppose this charge follows the circular path starting from point A as shown in the following figure.

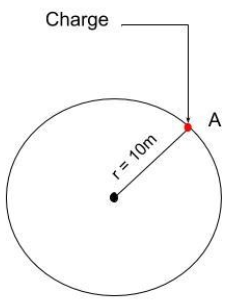
We know that the potential difference between any two points is the work done to move a charge between these two points. So the mathematical relation between voltage or potential difference is given below.
$V = \dfrac{W}{Q}$
Where, V is the voltage, W is the work required to move the charge, and Q is the charge to be moved. Hence, the work done is given by,
$W = VQ$……(1)
Now as we know while travelling in a circular path to traverse the path once, the charge will start from point A and will also end at point A. Since the start and end point is one and the same, so the potential difference will be zero (V = 0). Hence, from equation (1) the work done will become, zero. i.e option a is the correct answer.

Note: One volt of potential difference is obtained when 1 joule of work is done on a charge of one coulomb $1Volt = \dfrac{{1Joule}}{{1Coulomb}}$, i.e 1V= 1 J/C. Work done in moving a charge between any point in an electric field is independent of the path followed by the charge between the two points.