Question
Question: Evaluate the sum $\sum_{r=1}^{\infty} \frac{(2r-1)}{2^r}$...
Evaluate the sum ∑r=1∞2r(2r−1)
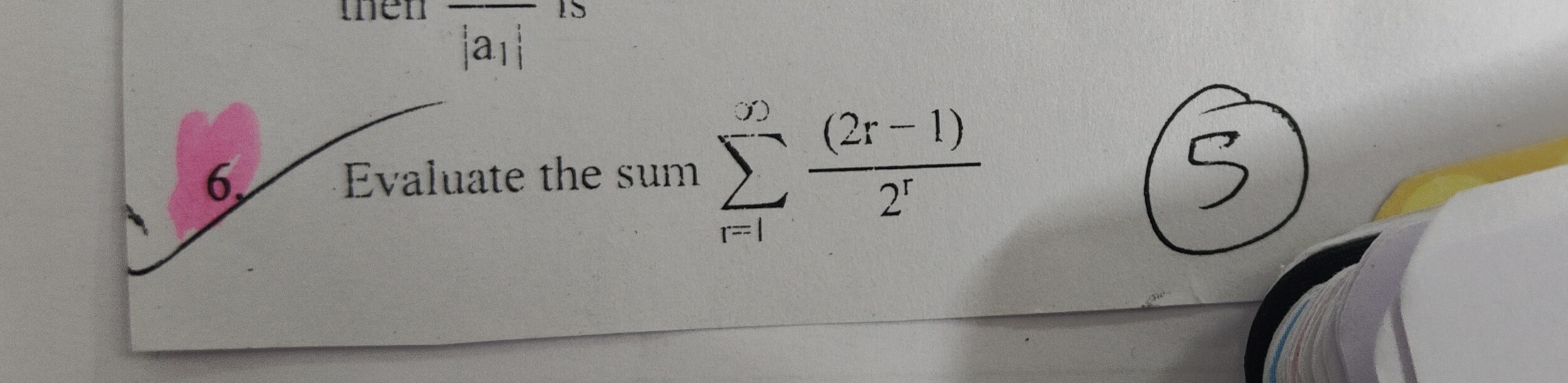
Answer
3
Explanation
Solution
The sum is an arithmetico-geometric series. Let S=∑r=1∞2r(2r−1).
Write out the series: S=21+43+85+167+….
Multiply by the common ratio 21: 21S=41+83+165+….
Subtract the second equation from the first: 21S=21+(43−41)+(85−83)+…
This simplifies to 21S=21+42+82+162+⋯=21+21+41+81+….
The terms 21+41+81+… form an infinite geometric series with first term a=21 and common ratio r=21. Its sum is 1−ra=1−1/21/2=1.
So, 21S=21+1=23.
Multiplying by 2, we get S=3.
