Question

The Zacchini family was renowned for their human-cannonball act in which a family member was shot from a cannon using either elastic bands or compressed air. In one version of the act, Emanuel Zacchini was shot over three Ferris wheels to land in a net at the same height as the open end of the cannon and at a range of $69m$ .He was propelled inside the barrel for $5.2m$ and launched at an angle of ${53^ \circ }$ .If his mass was $85kg$ and he underwent constant acceleration inside the barrel, what was the magnitude of the force propelling him? (Hint: Treat the launch as though it were along a ramp at ${53^ \circ }$ . (Neglect air drag.)

Answer 1

To solve this question, we must have a concept of projectile motion and here we firstly find the velocity at which the object is projected and then using Newton's law of motion we will find the acceleration and after we will draw the free body diagram and the solving for the net force and then we will get the required solution.

Formula used:
$R = \dfrac{{{v^2}\sin 2\theta }}{g}$
Where, $R$ is the range of the projectile, $v$ is the velocity and $g$ is the acceleration due to gravity.

Complete step by step answer:
According to the question we have the launched angle of the projectile is ${53^ \circ }$ and
The range of the projectile is $69m$. We know that the range of a projectile is given by $R = \dfrac{{{v^2}\sin 2\theta }}{g}$ and from here we can find the velocity of the launch projectile.
$R = \dfrac{{{v^2}\sin 2\theta }}{g} \\\ \Rightarrow v = \sqrt {\dfrac{{Rg}}{{\sin 2\theta }}} \\\$
Now simply substituting the value of in above equation and solving for the velocity of the launched projectile,
$v = \sqrt {\dfrac{{Rg}}{{\sin 2\theta }}} \\\ \Rightarrow v = \sqrt {\dfrac{{9.8 \times 69}}{{\sin 2\left( {{{53}^ \circ }} \right)}}} \\\ \Rightarrow v = 26.52m{\text{ }}{{\text{s}}^{ - 1}} \\\$
Now we know that the projectile is a two-dimensional motion so finding both the components,
${v_x} = v\cos \theta \\\ \Rightarrow {v_x} = 26.52\left( {\cos {{53}^ \circ }} \right) \\\ \Rightarrow {v_x} = 15.96 \\\$
Similarly other component,
${v_y} = v\sin \theta \\\ \Rightarrow {v_y} = 26.52\left( {\sin {{53}^ \circ }} \right) \\\ \Rightarrow {v_y} = 21.18 \\\$
According to the question, it is given that the acceleration is constant so we can easily find the acceleration using the formula of equations of motion.And we have,
$v = 26.52$
$\Rightarrow u = 0$
$\Rightarrow s = 5.2$
Now, using ${v^2} = {u^2} + 2as$ and substituting all the values and solving for acceleration,
${\left( {26.52} \right)^2} = {0^2} + 2 \times a \times 5.2 \\\ \Rightarrow a = \dfrac{{703.31}}{{2 \times 5.2}} \\\ \Rightarrow a = 67.63 \\\$
Now, we have to find the force propelling the body,
We have,
$m = 85\,kg$
$\Rightarrow a = 67.63$ and
We have to find the net force so we will first draw the diagram and the solve all the forces,

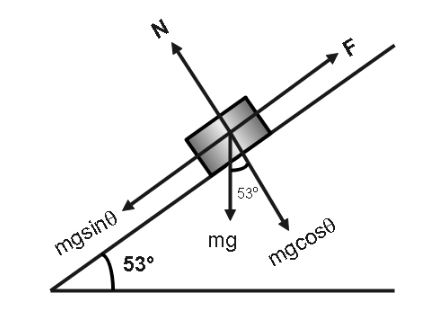
From the diagram we can see that,
$F = ma$
And
${F_{net}} = F - mg\sin \theta \\\ \Rightarrow F - 85 \times 9.8 \times \sin {53^ \circ } = 85 \times 67.63 \\\$
And hence solving above we will get our required solution.

\Rightarrow F = 85 \times 9.8 \times \sin {53^ \circ } + 85 \times 67.63 \\\ \Rightarrow F = 665.26 + 5748.55 $$ $\therefore F = 6413.81\,N$ **Hence, the magnitude of the force propelling him is $F = 6413.81\,N$ or $$F = 6.4 \times {10^3}\,N$$.** **Note:** For simplifying you must draw the free body diagram as if you will not draw there are chances you will end up making mistakes. Must remember the formulas of projectile motion as with the help of the range formula here we have solved for the velocity and you can only apply equations of motions if there is constant acceleration.