Question

The young’s modulus of a rubber string $8cm$ long and density $1.5kg/{m^3}$is $5 \times {10^8}N/{m^2}$, is suspended on the ceiling in a room. The increase in length due to its own weight will be:-
A. $9.6 \times {10^{ - 5}}m$
B. $9.6 \times {10^{ - 11}}m$
C. $9.6 \times {10^{ - 3}}m$
D. $9.6m$

Answer 1

Concept of relation between young’s modulus and change in length is used.

Formula used: $\Delta l = \dfrac{{{l^2}dg}}{{2y}}$

Complete step by step solution:
Let us consider a rope or rubber band of length $8cm$ as given in the question

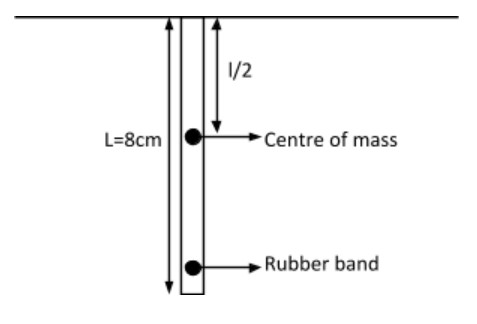
As the rope is of length, $l$. Its weight will act downward and there will be increase in its length from centre of mass i.e. $l/2$
We know that the relation between young’s modulus and change in length is given by
$y = \dfrac{F}{A} \times \dfrac{l}{{\Delta l}}$
But here $l \ to l/2$
So, $y = \dfrac{F}{A} \times \dfrac{l}{{2\Delta l}}$
$\Rightarrow \Delta l = \dfrac{{fl}}{{2AY}}$…………. (i)
Now, density, $d = \dfrac{{Mass}}{{Volume}}$
i.e. $d = \dfrac{M}{V}$
$d = \dfrac{M}{{Al}}$ (as volume$=$area$\times$length of rope or rubber band)
$\Rightarrow A = \dfrac{M}{{dl}}$……….. (II)
Also, force, $F = mg$…………. (III)
Where $g$ is acceleration due to gravity and $g = 10m/{s^2}$
Put (II) and (III) in (I), we get

$$\Delta l = \dfrac{{mg \times l}}{{2 \times \dfrac{m}{{dl}}}} \times Y \\\ \Rightarrow \Delta l = \dfrac{{mgldl}}{{2my}} \\\ \Rightarrow \Delta l = \dfrac{{{l^2}dg}}{{2Y}} \\\$$

Given that,
Length of rubber band, $l = 8cm$
$= 0.08m$
Density, of rubber band, $d = 1.5kg/{m^3}$
Young’s modulus, $Y = 5 \times {10^8}N/{M^2}$

The reaction for increase in length and young’s modulus is as follows,
$\Delta l = \dfrac{{{l^2}dg}}{{2Y}}$
Where
$\Delta l =$Increase in length of rubber band due to its own weight
$d =$Density of rubber band
$g =$Acceleration due to gravity $= 10m/{s^2}$
$Y =$Young’s modulus of rubber band
$l =$Original length of rubber band.
So, as $\Delta l = \dfrac{{{l^2}dg}}{{2Y}}$
$\Delta l = \dfrac{{\left( {8 \times {{10}^{ - 2}}} \right) \times 1.5 \times 10}}{{2 \times 5 \times {{10}^8}}}$

$$\Delta l = \dfrac{{64 \times {{10}^{ - 4}} \times 1.5 \times 10}}{{{{10}^9}}} \\\ \Delta l = 96 \times {10^{ - 12}} \\\ \Delta l = 9.6 \times {10^{ - 11}}m \\\$$

Hence, the correct option is (B).

Note: Before solving the question, we must consider the change in length of the rubber band due to its weight which will cause it to move away from the centre of mass. So, half-length is taken but in density, total length of rubber band is considered as density is due to mass and length of overall rubber band.