Question

The YDSE is done in a medium of refractive index 4/3. A light of wavelength 600 nm in vaccum is falling on the slits having 0.45 mm separation. The lower slit $S_2$ is covered by a thin glass sheet of thickness 10.4 µm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown

in figure.

The location of central maximum (in mm) on the y-axis from O is

Answer 1

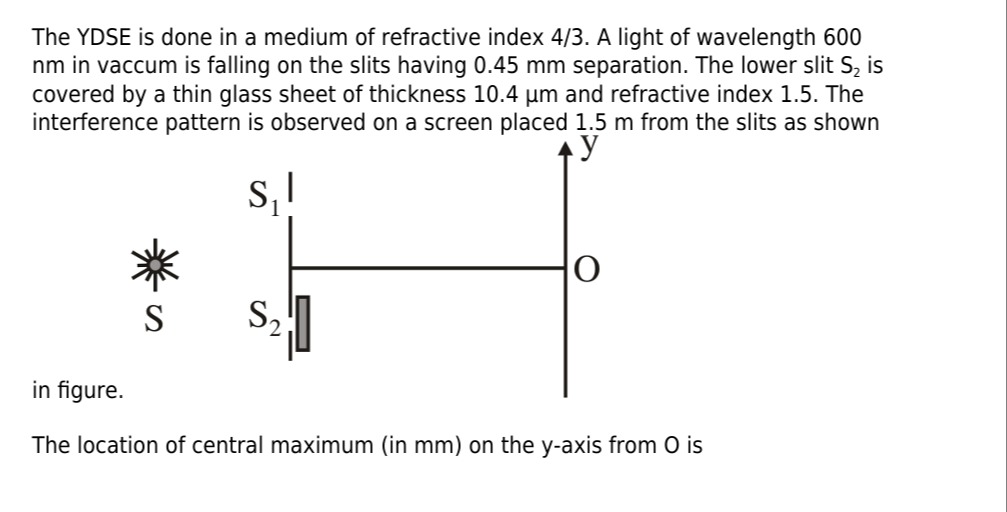
-4.33

Answer 2

The central maximum occurs at the point where the optical path difference between the waves from the two slits is zero. Let the refractive index of the medium be $n_m = 4/3$. The lower slit $S_2$ is covered by a thin glass sheet of thickness $t = 10.4$ µm $= 10.4 \times 10^{-6}$ m and refractive index $n_g = 1.5$. The slit separation is $d = 0.45$ mm $= 0.45 \times 10^{-3}$ m. The screen is placed at a distance $D = 1.5$ m from the slits.

Consider a point P on the screen at a vertical distance $y$ from the point O directly opposite the midpoint of the slits. The geometric path length from $S_1$ to P is $r_1$ and from $S_2$ to P is $r_2$. In the medium, the optical path length from $S_1$ to P is $n_m r_1$. The light from $S_2$ travels through the sheet of thickness $t$ and then through the medium for the remaining distance. The geometric path length in the medium is $r_2 - t$, and in the glass sheet is $t$. The optical path length from $S_2$ to P is $n_m (r_2 - t) + n_g t$. The optical path difference between the two waves at P is:

$\Delta OP = \text{Optical path from } S_2 \text{ to } P - \text{Optical path from } S_1 \text{ to } P$ $\Delta OP = (n_m (r_2 - t) + n_g t) - n_m r_1$ $\Delta OP = n_m r_2 - n_m t + n_g t - n_m r_1$ $\Delta OP = n_m (r_2 - r_1) + (n_g - n_m)t$.

For the central maximum, the optical path difference is zero: $\Delta OP = 0$ $n_m (r_2 - r_1) + (n_g - n_m)t = 0$.

For a point P at a distance $y$ from O, the geometric path difference $r_2 - r_1$ is approximately $y d / D$ for small angles (which is usually the case in YDSE). If y is positive (above O), $r_2 > r_1$, so $r_2 - r_1 = y d / D$. If y is negative (below O), $r_1 > r_2$, so $r_2 - r_1 = -|y| d / D = y d / D$. Thus, the approximation $r_2 - r_1 \approx y d / D$ holds for both positive and negative y.

Substituting $r_2 - r_1 = y d / D$ into the equation for the central maximum: $n_m (y d / D) + (n_g - n_m)t = 0$ $n_m (y d / D) = -(n_g - n_m)t$ $y = -\frac{(n_g - n_m)t D}{n_m d} = \frac{(n_m - n_g)t D}{n_m d}$.

Given values: $n_m = 4/3$ $n_g = 1.5 = 3/2$ $t = 10.4 \times 10^{-6}$ m $D = 1.5$ m $d = 0.45 \times 10^{-3}$ m

Calculate $n_m - n_g$: $n_m - n_g = 4/3 - 3/2 = 8/6 - 9/6 = -1/6$.

Substitute the values into the formula for $y$: $y = \frac{(-1/6) \times (10.4 \times 10^{-6} \text{ m}) \times (1.5 \text{ m})}{(4/3) \times (0.45 \times 10^{-3} \text{ m})}$ $y = \frac{-1 \times 10.4 \times 1.5}{6} \times \frac{3}{4 \times 0.45} \times \frac{10^{-6} \times 1.5}{10^{-3} \times 0.45}$ $y = \frac{-10.4 \times 1.5 \times 3}{6 \times 4 \times 0.45} \times 10^{-3}$ $y = \frac{-10.4 \times 4.5}{10.8} \times 10^{-3}$ $y = \frac{-46.8}{10.8} \times 10^{-3}$ $y = -\frac{468}{108} \times 10^{-3}$ Divide by 4: $y = -\frac{117}{27} \times 10^{-3}$ Divide by 9: $y = -\frac{13}{3} \times 10^{-3}$ $y \approx -4.333... \times 10^{-3}$ m

Convert to mm: $y \approx -4.333...$ mm.

The location of the central maximum on the y-axis from O is approximately -4.33 mm. The negative sign indicates that the central maximum is below O.