Question

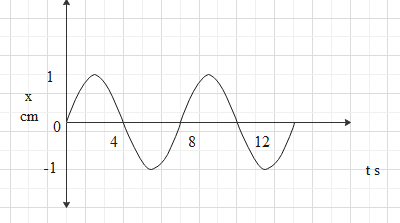
The $x - t$ graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at $t = \dfrac{4}{3}s$ is

A $\dfrac{{\sqrt 3 }}{{32}}{\pi ^2}\,cm/{s^2}$
B. $\dfrac{{ - {\pi ^2}}}{{32}}\,cm/{s^2}$
C. $\dfrac{{{\pi ^2}}}{{32}}\,cm/{s^2}$
D. $- \dfrac{{\sqrt 3 }}{{32}}{\pi ^2}\,cm/{s^2}$

Answer 1

From the graph we can see that the displacement given is a sine function. So we can write it in the form $x = A\sin \omega t$ . We know that $\omega = \dfrac{{2\pi }}{T}$ Where, $\omega$ is the angular frequency and $T$ is the time period. substitute this value in the displacement equation. And then, acceleration can be found by taking the second derivative of displacement with respect to time.

Complete step by step answer:
By analysing the graph given we can find that the displacement given is a sine function. So we can write it in the form
$x = A\sin \omega t$
Where $A$ denotes the amplitude of the wave and $\omega$ is the angular velocity and $t$ denotes the time.
We know that angular velocity and time period is inversely related. The relation is given as
$\omega = \dfrac{{2\pi }}{T}$
Where, $\omega$ is the angular frequency and $T$ is the time period.
Time period is the time taken to complete one oscillation.
Now let us substitute the value of $\omega$ in the equation for displacement. Then we get,
$x = A\sin \,\dfrac{{2\pi }}{T}t$
Let us find the time period from the given graph. One crest and trough together in the graph represent one complete oscillation. Therefore we can take time for one complete oscillation as $8\,s$. So this is the time period.
Thus, $T = 8\,s$
So,
$x = A\sin \dfrac{{2\pi }}{8}t$
$\Rightarrow x = A\sin \dfrac{\pi }{4}t$
We need to find acceleration at $t = 4/3s$
We can find acceleration by finding the second derivative of displacement.
This is because acceleration is the change in velocity by time taken. Given as
$a = \dfrac{{dv}}{{dt}}$ where $v$ is the velocity and velocity is the change in displacement by time taken
$v = \dfrac{{dx}}{{dt}}$. By substituting this value of $v$ in $a$ we get
$a = \dfrac{{{d^2}x}}{{d{t^2}}}$
let us first find $\dfrac{{dx}}{{dt}}$
$\dfrac{{dx}}{{dt}} = \dfrac{{d\left( {A\sin \dfrac{\pi }{4}t} \right)}}{{dt}}$
$\Rightarrow \dfrac{{dx}}{{dt}} = A\,\cos \dfrac{\pi }{4}t \times \dfrac{\pi }{4}$
Now, let us find the second derivative of displacement with respect to time.
$\dfrac{{{d^2}x}}{{d{t^2}}} = \dfrac{d}{{dt}}\left( {\dfrac{{dx}}{{dt}}} \right)$
Let us substitute the value of $\left( {\dfrac{{dx}}{{dt}}} \right)$ in this equation.
$\Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} = \dfrac{d}{{dt}}\left( {A\cos \,\dfrac{\pi }{4}t \times \dfrac{\pi }{4}} \right)$
$\Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} = \dfrac{{ - A\pi }}{4}\,\sin \dfrac{\pi }{4}t \times \dfrac{\pi }{4}$
We have $t = \dfrac{4}{3}s$ , Also, amplitude $A$ is the maximum displacement. From the graph we can see that the maximum value of displacement is one .
$\therefore A = 1\,cm$
On substituting these values in equation we get
$\Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} = \dfrac{{ - {\pi ^2}}}{{16}}\sin \dfrac{\pi }{4} \times \dfrac{9}{3}$
$\Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} = \dfrac{{ - {\pi ^2}}}{{16}} \times \dfrac{{\sqrt 3 }}{2}$
$\Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} = \dfrac{{ - \sqrt 3 {\pi ^2}}}{{32}}\,cm/{s^2}$
$\therefore a = \dfrac{{{d^2}x}}{{d{t^2}}} = \dfrac{{ - \sqrt 3 {\pi ^2}}}{{32}}\,cm/{s^2}$
This is the acceleration for the given time.
So, the correct answer is option D.

Note: We took the displacement as a sine function since the graph given is a sine wave. Displacement as a sine function is given as $x = A\sin \omega t$ . Instead of sine wave if a cosine wave is given then the displacement should be written in the form $x = A\cos \omega t$ . So analyse the graph carefully before doing such problems.