Question

The work done in carrying a charge e from O to E is:

& \text{A}\text{. }\dfrac{\sqrt{2}qe}{\pi {{\varepsilon }_{0}}a} \\\ & \text{B}\text{. }\dfrac{qe}{\pi {{\varepsilon }_{0}}a}\left[ \dfrac{1}{\sqrt{5}}-1 \right] \\\ & \text{C}\text{. }\dfrac{qe}{\pi {{\varepsilon }_{0}}a}\left[ \dfrac{1}{\sqrt{5}}+1 \right] \\\ & \text{D}\text{. zero} \\\ \end{aligned}$$

Answer 1

Work done is given as force required to move an object from one place to another. In an electric field, the work done in carrying a charge from one place to another can be given as a potential difference at the two points times the charge. Hence by finding the potential at O and E we can calculate the work done.

Formula used:

& V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{r} \\\ & W=\left( {{V}_{a}}-{{V}_{b}} \right)Q \\\ \end{aligned}$$ **Complete step-by-step answer:** We have to find the work done in carrying a charge e from point O to E, for that let us redraw the draw as shown 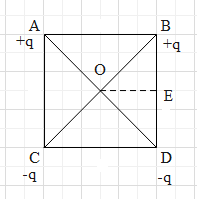 Now here we have consider the distance between AB, BD, CD and AC is so we can write $$AB=BD=CD=AC$$ From the diagram it is clear that the charges are placed in shape of square therefore the diagonals BC and AD will be equal $$BC=AD$$ Now the potential of an electric field is given as $$V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{r}$$ Where q is the charge at the point and r is the distance from the point. So potential at O can be given as $${{\text{V}}_{O}}\text{=}\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{+q}{OA}+\dfrac{q}{OB}+\dfrac{-q}{OC}+\dfrac{-q}{OD} \right]\text{ }..............\text{(i)}$$ Now from the diagram we can write $$\begin{aligned} & OB=OC=\dfrac{BC}{2} \\\ & OA=OD=\dfrac{AD}{2} \\\ \end{aligned}$$ As BC and AD are equal therefore, $$OB=OC=OA=OD$$, hence equation (i) becomes $$\begin{aligned} & {{\text{V}}_{O}}\text{=}\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{q}{OA}+\dfrac{q}{OA}-\dfrac{q}{OA}-\dfrac{q}{OA} \right] \\\ & {{\text{V}}_{O}}=0 \\\ \end{aligned}$$ Now let us find potential at E, which can be given as $${{\text{V}}_{E}}\text{=}\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{+q}{AE}+\dfrac{+q}{BE}+\dfrac{-q}{CE}+\dfrac{-q}{DE} \right]\text{ }...................\text{(ii)}$$ As E is the midpoint of BD, we can write $$BE=DE$$ And as it is square and E is midpoint of BE, therefore $$AE=CE$$ Now equation (ii) can be rewritten as $$\begin{aligned} & {{\text{V}}_{E}}\text{=}\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{q}{AE}+\dfrac{q}{BE}-\dfrac{q}{AE}-\dfrac{q}{BE} \right] \\\ & {{\text{V}}_{E}}=0 \\\ \end{aligned}$$ Work done in carrying a charge e from O to E, is given as $$W=\left( {{V}_{O}}-{{V}_{E}} \right)e$$ Substituting values of $${{V}_{O}}\text{ and }{{V}_{E}}$$we calculated above we get $$W=0$$ **So, the correct answer is “Option D”.** **Note:** The potential at center and at the midpoint of the sides of the square will be zero as if there are equal numbers of positive and negative charges. Work done is also given in terms of electric field that is work done will be equal to the line integral of the electric field multiplied with the charge. As the force is given as a product of charge and electric field.