Question

The work done by the frictional force on a surface in drawing a circle of radius r on the surface by a pencil of negligible mass with a normal pressing force N (coefficient of friction ${\mu _k}$) is:
A) $4\pi {r^2}{\mu _k}N$
B) $- 2\pi {r^2}{\mu _k}N$
C) $- 2\pi r{\mu _k}N$
D) Zero

Answer 1

In this question, the concept of friction force is applied, that is the friction force is the product of the coefficient of friction and the normal force exerted on the body or the object. First, draw the diagram using all the information given in the question and then find out the work done by the frictional force in drawing a circle of radius and discuss the derivation.

Complete step by step answer:
As per the given question first, we will draw the diagram as per the given situation.

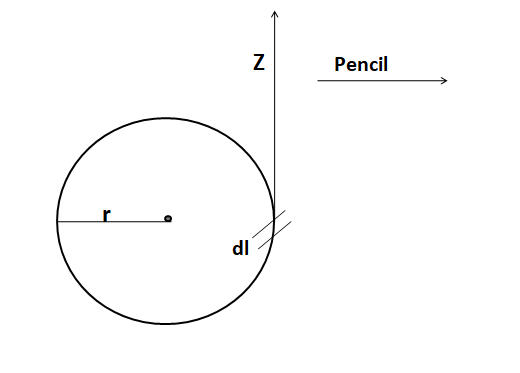
The motion of the pencil is in the $z$ direction. The given radius of the circle is $r$. The friction of motion will be tangentially.
So, we have to derive the work done at $dl$ length.
We know that the work done at length $dl$ can be written as
${\rm{dw = }}\;{\rm{ - }}{{\rm{f}}_k}.dl$
Here, the force of friction is ${{\rm{f}}_k}$.
As we know that the frictional force is always opposing the relative motion of the body so it is negative. Now, we integrate the above equation as,
$\int {dw\; = \;w}$
$\Rightarrow \;w\, = - \int {{{\rm{f}}_k}.dl}$
We know that the friction force is the product of the coefficient of friction and the normal force exerted on the body or the object so,
${{\rm{f}}_k}\; = \;{\mu _k}{\rm{k}}$
Where, ${\mu _k}$is coefficient of friction and N is the pressing force.
Now we will substitute the value of friction force in the work done equation as,
$w\; = \, - \int {{\mu _k}{\rm{Ndl}}}$
The total length of the circle is $2\pi r$ . So to find out the total work done at length $dl$,we have to integrate from $0$ to $2\pi r$, so the above equation become,
$w\, = \, - \int\limits_0^{2\pi r} {{\mu _k}{\rm{Ndl}}}$
We integrate the above equation as,
$w\, = \, - {\mu _k}{\rm{N}}\left[ {2\pi r - 0} \right]$
$w\, = \, - 2\pi r{\mu _k}N$

Hence the correct option is (C).

Note: When a body is dragged along a rough surface, the frictional force will be acting in the direction opposite to the displacement of the body. And the angle between the displacement of the body and frictional force will be $180^\circ$. Hence the total work done by the frictional force will be negative.