Question

The work done by the force $\vec F = A({y^2}\hat i + 2{x^2}\hat j)$, where A is a constant and x and y are in meters around the path shown is

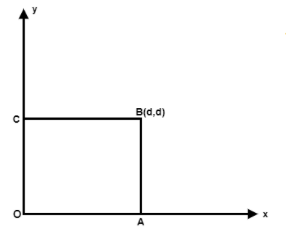
A) Zero.
B) $Ad$.
C) $A{d^2}$.
D) $A{d^3}$.

Answer 1

Work is done when a force that is applied to an object moves that object. The work is calculated by multiplying the force by the amount of movement of an object $W = F * D$, where W= work done, F= force applied and D= displacement.

Complete step by step answer:
To calculate the work done let us consider some points along the path. Let, these be O, A, B, and C where, O is the initial point and C is the final point. So, the body moves from O to A, then from A to B, from B to C, and finally from C to O.

Let us calculate a small work done at any random point between O and A. This can be written as,
$dW = \overrightarrow F .\overrightarrow {dr}$, where $\overrightarrow {dr}$ is a small displacement along OA.
Again, $\overrightarrow {dr}$ can be written as $\overrightarrow {dr} = dx\hat i + dy\hat j$.
So, we can write the small work done for this displacement as $dW = A({y^2}\hat i + 2{x^2}\hat j).(dx\hat i + dy\hat j) = A({y^2}dx + 2{x^2}dy)$
Now, to find total work done along OA can we given by,
${W_{OA}} = \int {dW} = A\int {{y^2}dx} + 2{x^2}dy$.
But, y=0 along OA. So, we have,
${W_{OA}} = A\int\limits_0^0 {2{x^2}dy} = 0$.
Similarly, we can write,
${W_{AB}} = A\int {{y^2}dx} + 2{x^2}dy$.
Now x =d is constant so $dx = 0$.
Thus, we can write,
${W_{AB}} = A\int {{y^2}0} + 2{d^2}dy = 2A{d^2}\int\limits_0^d {dy} = 2A{d^3}$.
Along BC we get,
${W_{BC}} = A\int {{y^2}dx} + 2{x^2}dy$.
Now y =d is constant so $dy = 0$.
So, ${W_{BC}} = A{d^2}\int\limits_d^0 {dx} = - A{d^3}$.
For the path C0 we can write,
${W_{CO}} = A\int {{y^2}dx} + 2{x^2}dy$. Now x =0 is constant so $dx = 0$.
Thus, ${W_{CO}} = A.0 = 0$.
Finally, the total work done is
${W_{Total}} = {W_{OA}} + {W_{AB}} + {W_{BC}} + {W_{CO}}$.
Putting the values previously calculated we get,
${W_{Total}} = 0 + 2A{d^3} - A{d^3} + 0 = A{d^3}$.
So, the total work done is $A{d^3}$.

Thus, the right answer is option (D).

Note: The most common mistake done in this type of problem is done while taking the integration. Please take great care while putting in the limit. Also, special care has to be taken about the values of x and y at different points. If we make even a small mistake for any of these values than the solution will give us a different output altogether.