Question

The work done by a body on the application of a constant force is directly proportional to the distance traveled by the body. Express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Read from the graph, the work is done when the distance traveled by the body is 0 unit.
(a) 0 unit
(b) 2 units
(c) 1 unit
(d) 3 units

Answer 1

For solving first we will understand the basic concept of defining work done by a force on the body mathematically and for better understanding, we will see how we can find the work done by a force using graphs. After that, we will easily solve for the correct answer to this question.

Complete step-by-step solution:
Given:
It is given that the work done by a body on the application of a constant force is directly proportional to the distance traveled by the body. And we have to plot the graph for the case when the constant force of 5 units is applied to the body and calculate the work done when the distance traveled by the body is 0 unit.
Now, before we proceed we should know the concept of calculating work done by the body when force $\overrightarrow{F}$ units acts on a body and displacement of the body is $\overrightarrow{x}$ units.
Work-done by force $\overrightarrow{F}$ :
Work done by the force on a body is given by the dot product of force vector and displacement vector. Then,
Mathematically the work done by the force $\overrightarrow{F}=W=\left( \overrightarrow{F} \right)\bullet \left( \overrightarrow{x} \right)$ . Where $\overrightarrow{x}$ is the displacement of the body due to the force $\overrightarrow{F}$ .
Now, in other form, we can also write work $W=\int\limits_{{{x}_{initial}}}^{{{x}_{final}}}{\left( \overrightarrow{F} \right)}\bullet \left( \overrightarrow{dx} \right)$ . Where $\overrightarrow{dx}$ is the small displacement caused by force $\overrightarrow{F}$ . Here, we can express force as a function of displacement and integrate it to calculate the work done for the given displacement. We can interpret work to be the area under the curve of the plot of force $\overrightarrow{F}$ and displacement $\overrightarrow{x}$ . The graphical representation of this is given below:

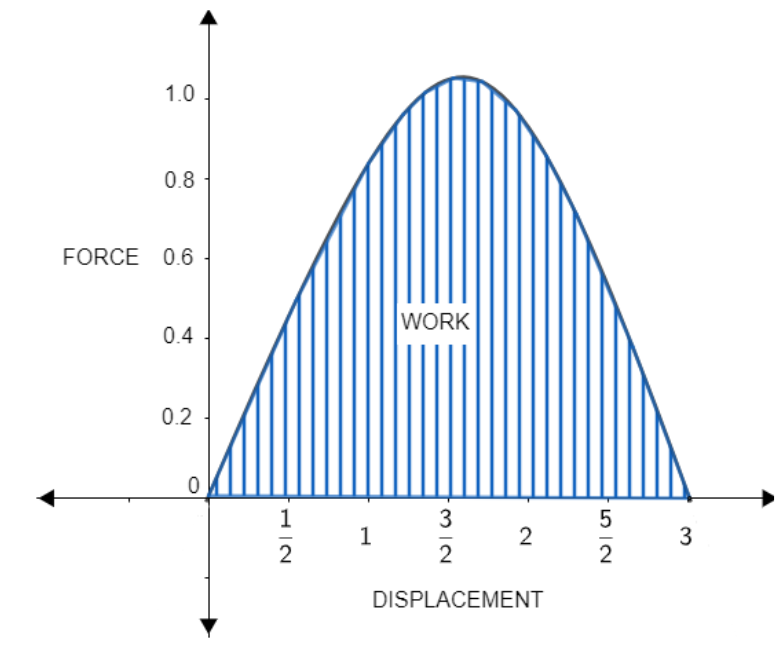
Now, we have understood how to find the work if we know the force vector $\overrightarrow{F}$ and displacement vector $\overrightarrow{x}$.
Now, we come back to our question where we have a force of magnitude $\left| \overline{F} \right|$ = 5 units, and we have to find the work.
Let, $\overrightarrow{x}$ is the displacement in the direction of force then, $\overrightarrow{F}\centerdot \overrightarrow{x}=\left| \overrightarrow{F} \right|\left| \overrightarrow{x} \right|$ .Then,
Work $=\left| \overrightarrow{F} \right|\left| \overrightarrow{x} \right|=5x$ units.
Now, the plot of force and displacement for this case is given below:

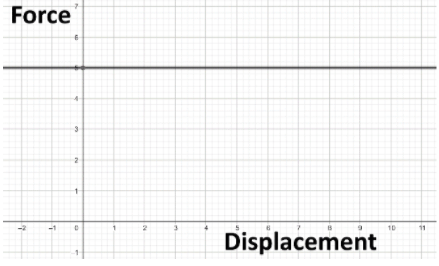
Now, from the above plot, we can say that for this case the plot will be a straight line parallel to the displacement axis. And for the zero displacement, the value of work done by the body will be zero as the area under the curve will be zero.
Hence, (a) is the correct option.

Note: Here, the student should apply the concept of work done by a force correctly. Although this problem is very easy and even if the displacement of the body is non-zero then also with the vector approach we can solve it or by making the force versus displacement plot we can find the work done by calculating the area under the curve.