Question

The wheel of radius $r = 300{\rm{ mm}}$ rolls to the right without slipping and has a velocity ${V_0} = 3{\rm{ m/s}}$ of its centre $O$. The speed of the point $A$ on the wheel for the instant represented in the figure is :-

(A) $4.36{\rm{ m/s}}$
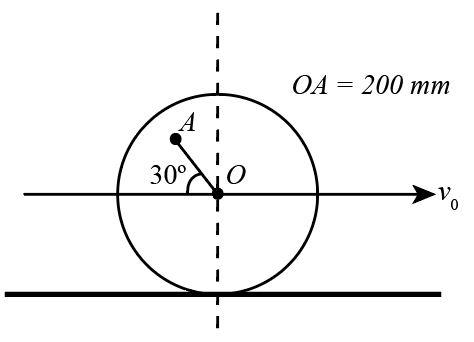
(B) ${\rm{5 m/s}}$
(C) ${\rm{3 m/s}}$
(D) ${\rm{1}}{\rm{.5 m/s}}$

Answer 1

This question is based on the relationship between the linear velocity and the angular velocity of a point on a wheel rolling on a surface without slipping. When two velocity vectors ${V_1}$ and ${V_2}$ are acting on a point in such a way that the angle between them is $\theta$ then the net velocity vector of that point is calculated by Parallelogram Theorem. The formula for the net velocity is given by-
${V_{net}} = \sqrt {{{\left( {{V_1}} \right)}^2} + {{\left( {{V_2}} \right)}^2} + 2{V_1}{V_2}\cos \theta }$

Complete step by step solution
Given:
The radius of the wheel
$r = 300{\rm{ mm}}\\\ {\rm{or,}}\\\ {\rm{r = 0}}{\rm{.3 m}}$
The linear velocity of the centre $O$ of the wheel ${V_0} = 3{\rm{ m/s}}$
And the distance between the centre of the wheel $O$ and point $A$ on the wheel
$OA = 200{\rm{ mm}}\\\ {\rm{or,}}\\\ {\rm{OA = 0}}{\rm{.2 m}}$
The angle between $OA$ and the horizontal $\theta = 30^\circ$
We know the relation between the linear velocity and the angular velocity of a point moving in a circular motion is given by-
${V_0} = \omega r$
Where, $\omega$ is the angular velocity of the wheel and $r$ is the radius of the wheel.
Now substituting the values of ${V_0}$ and $r$ in the equation we get,
$3{\rm{ m/s}} = \omega \times 0.3{\rm{ m}}\\\ \omega = \dfrac{3}{{0.3}}$
Solving this we get,
$\omega = 10{\rm{ rad/s}}$
Now, using the relation, the linear velocity of the point $A$ on the wheel is given by-
${V_A} = \omega \times OA$
Substituting the values of $\omega$ and $OA$ in the equation we get,
${V_A} = 10 \times 0.2\\\ {V_A} = 2{\rm{ m/s}}$
Net velocity of the point $A$ can be calculated by-
${V_{net}} = \sqrt {{{\left( {{V_0}} \right)}^2} + {{\left( {{V_A}} \right)}^2} + 2{V_0}{V_A}\cos \theta }$
Substituting the values of ${V_0}$, ${V_A}$ and $\theta$ in the equation we get,
${V_{net}} = \sqrt {{{\left( 3 \right)}^2} + {{\left( 2 \right)}^2} + 2 \times 3 \times 2 \times \cos 30^\circ } \\\ \Rightarrow {V_{net}} = \sqrt {9 + 4 + 12 \times \dfrac{1}{2}} \\\ \Rightarrow {V_{net}} = \sqrt {19} \\\ \Rightarrow {V_{net}} = 4.36{\rm{ m/s}}$
Therefore, the speed of the point $A$ on the wheel is $4.36{\rm{ m/s}}$ and the correct option is –
(A) $4.36{\rm{ m/s}}$

Note:
It should be noted that the direction of the velocity of the center of the wheel $O$ is parallel to the horizontal surface while the direction of the point $A$ on the wheel is radially outwards at an angle of $30^\circ$ from the horizontal.