Question
Question: The volume (V) of a monatomic gas varies with its temperature (T), as shown in the graph. The ratio ...
The volume (V) of a monatomic gas varies with its temperature (T), as shown in the graph. The ratio of work done by the gas to the heat absorbed by it, when it undergoes a change from state A to state B, is?
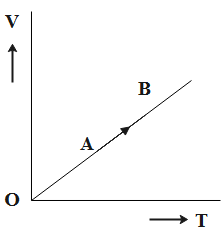
A.31
B.52
C.72
D.32
Explanation
Solution
This problem is a direct question. We will make use of the specific heat at a constant pressure of monatomic gas and substitute the same value in the equation of heat absorbed. Then we will divide this equation by the equation of the work done in the case of the isobaric process. Thus, we will get the required ratio.
Complete step-by-step solution
From given problem, we have a monatomic gas, so, we have,
CP=25R
Or we can compute the specific heat at constant pressure as follows.
