Question

The volume of the largest possible right circular cylinder that can be inscribed in a sphere of radius = $\sqrt 3$ is:-
A. $\dfrac{4}{3}\sqrt 3 \pi$
B. $2\pi$
C. $\dfrac{8}{3}\sqrt 3 \pi$
D. $4\pi$

Answer 1

Here in this question two concepts will get which are mentioned below:-
1. Volume of a cylinder = $\pi {r^2}h$ (where ‘r’ is the radius of cylinder and ‘h’ is the height of the cylinder)
2. Condition for maxima:-A function f(x) has a local maxima or local maximum value at a point $x_0$ if the values of f(x) of f for ‘x’ near $x_0$ are all less than f($x_0$). We can find maxima of a function f on an interval [a,b] as follows:-

*Solve $f'(x) = 0$ to find critical points of ‘f’

*Now double derivative the function and check if it is less than zero then there will

be maximum value at that critical point.

Complete step-by-step answer:
Draw a sphere of radius $\sqrt 3$ having a cylinder inscribed in it having radius ‘r’ and height ‘h’.

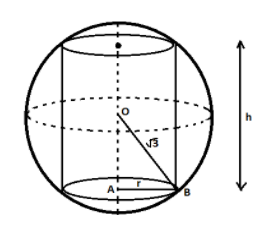
Now in triangle AOB, we will apply Pythagoras theorem as $\angle OAB = {90^ \circ }$
$\Rightarrow O{A^2} + A{B^2} = O{B^2}$
Now we will put values of OA = half of the cylinder height, OB = radius of sphere given $\sqrt 3$, AB = radius of a cylinder.
$\Rightarrow {(\dfrac{h}{2})^2} + {r^2} = {(\sqrt 3 )^2}$
$\Rightarrow {\dfrac{h}{4}^2} + {r^2} = 3$
$\Rightarrow {r^2} = 3 - {\dfrac{h}{4}^2}$ ......................... (Equation 1)
Now Volume of a cylinder = $\pi {r^2}h$ (where ‘r’ is the radius of cylinder and ‘h’ is the height of the cylinder)
$\Rightarrow V = \pi (3 - {\dfrac{h}{4}^2})h$ (From equation 1)
$\Rightarrow V = \pi (3h - {\dfrac{h}{4}^3})$ (Multiplying h inside) ....................... (Equation 2)
Now we will derive V in terms of ‘h’
$\Rightarrow V' = \pi (3 - {\dfrac{{3h}}{4}^2})$
For maximum condition we will put $V' = 0$
$\Rightarrow \pi (3 - {\dfrac{{3h}}{4}^2}) = 0$
$\Rightarrow 3 = {\dfrac{{3h}}{4}^2}$
Now we will cancel 3 from both sides and then solve for value of ‘h’
$\Rightarrow {h^2} = 4$
$\Rightarrow h = \pm 2$
Now we will check condition of maxima by doing double derivative of the function with respect to ‘h’
$\Rightarrow V'' = 0 - \dfrac{{6h}}{4}$
$\Rightarrow V'' = - \dfrac{{6h}}{4}$
As $V'' < 0$ this is the condition for local maxima, therefore maximum value will be obtained by putting $h = 2$ in equation 1
$\Rightarrow V = \pi (3 - {\dfrac{2}{4}^2})2$
$\Rightarrow V = \pi (3 - 1)2$
$\Rightarrow V = 4\pi$

So, the correct answer is “Option D”.

Note: Students may likely to make mistake while determining whether it is a case of maxima or minima so here below brief explanation is mentioned:-
Condition of maxima is mentioned in hints.
Condition for minima:-A function f(x) has local minima at a point $x_0$ if the values of f(x) of f for ‘x’ near $x_0$ are all greater than f($x_0$). We can find minima of a function f on an interval [a,b] as follows:-
*Solve $f'(x) = 0$ to find critical points of ‘f’
*Now double derivative the function and check if it is greater than zero then there will be
minimum value at that critical point.