Question

The volume of solid obtained by revolving the area of the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ about major and minor axes are in the ratio.

Answer 1

In this question, we are given equation of ellipse as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. We need to find the ratio of volume of solid obtained by revolving the area of the ellipse about major and minor axes. Center of the ellipse is at origin, so we will find a volume of solid revolving about the x axis and y axis. Volume of any solid revolving an area given by equation g(x,y) about x axis is equal to $\int\limits_{a}^{b}{\pi {{y}^{2}}}dx$ where y = f(x) and a,b are points on x axis where g(x,y) cuts. Similarly, about y axis volume is equal to $\int\limits_{a}^{b}{\pi {{x}^{2}}}dy$ where x = f(y) and a,b are points on y axis where g(x,y) cuts.

Complete step by step answer:
Here we are given the equation of the ellipse as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.
Let us first draw a diagram for this ellipse. We have,

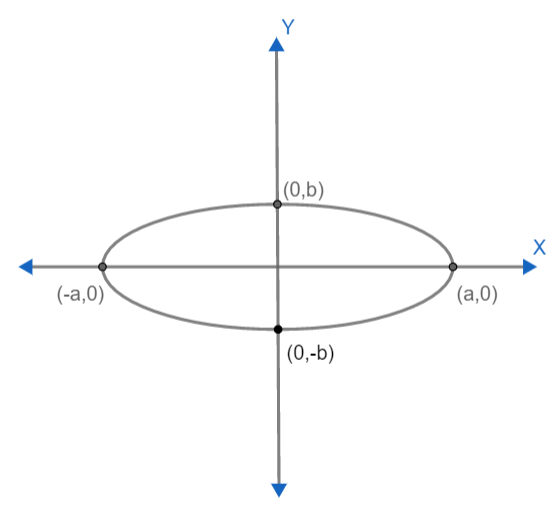
We need to find the volume of solid obtained by revolving the area of the ellipse about the major axis and minor axis. From the diagram we can see that, the major axis is the x axis and minor axis is the y axis.
We know volume of solid when equation g(x,y) is revolved about x axis is given by $v=\int\limits_{a}^{b}{\pi {{y}^{2}}}dx$ where y = f(x), a,b are points where g(x,y) cuts x axis.
So let us use this formula, here $g\left( x,y \right)=\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.
Calculating value of ${{y}^{2}}$ we get,
$\dfrac{{{y}^{2}}}{{{b}^{2}}}=1-\dfrac{{{x}^{2}}}{{{a}^{2}}}\Rightarrow {{y}^{2}}={{b}^{2}}\left( 1-\dfrac{{{x}^{2}}}{{{a}^{2}}} \right)\Rightarrow {{y}^{2}}={{b}^{2}}-\dfrac{{{b}^{2}}{{x}^{2}}}{{{a}^{2}}}$.
From diagram a,b are -a,a respectively, so we have
$v=\int\limits_{-a}^{a}{\pi \left( {{b}^{2}}-\dfrac{{{b}^{2}}{{x}^{2}}}{{{a}^{2}}} \right)}dy$.
We know $\int{{{x}^{n}}}dx=\dfrac{{{x}^{n+1}}}{n+1}\text{ and }\int{1\cdot dx}=x$ so we have,

& v=\left[ \pi {{b}^{2}}x-\dfrac{\pi {{b}^{2}}}{{{a}^{2}}}\dfrac{{{x}^{2+1}}}{2+1} \right]_{-a}^{a} \\\ & \Rightarrow v=\left[ \pi {{b}^{2}}x-\dfrac{\pi {{b}^{2}}}{{{a}^{2}}}\dfrac{{{x}^{3}}}{3} \right]_{-a}^{a} \\\ \end{aligned}$$. Solving further we get, $$\begin{aligned} & \Rightarrow v=\left[ \pi {{b}^{2}}a-\dfrac{\pi {{b}^{2}}}{{{a}^{2}}}\dfrac{{{a}^{3}}}{3}-\left( \pi {{b}^{2}}\left( -a \right)-\dfrac{\pi {{b}^{2}}}{{{a}^{2}}}\dfrac{{{\left( -a \right)}^{3}}}{3} \right) \right] \\\ & \Rightarrow \left[ \pi {{b}^{2}}a-\dfrac{\pi {{b}^{2}}a}{3}+\pi {{b}^{2}}a-\dfrac{\pi {{b}^{2}}a}{3} \right] \\\ & \Rightarrow 2\pi {{b}^{2}}a-\dfrac{2\pi {{b}^{2}}a}{3} \\\ & \Rightarrow \dfrac{4\pi {{b}^{2}}a}{3} \\\ \end{aligned}$$ Here volume is $\dfrac{4\pi {{b}^{2}}a}{3}$ when revolved around the major axis. When a solid is revolved around y axis we have the formula $v=\int\limits_{a}^{b}{\pi {{x}^{2}}}dy$. Let us find the value of ${{x}^{2}}$. $$\dfrac{{{x}^{2}}}{{{a}^{2}}}=1-\dfrac{{{y}^{2}}}{{{b}^{2}}}\Rightarrow {{x}^{2}}={{a}^{2}}-\dfrac{{{a}^{2}}{{y}^{2}}}{{{b}^{2}}}$$. From diagram a,b are -b, b respectively so we have, $v=\int\limits_{-b}^{b}{\pi \left( {{a}^{2}}-\dfrac{{{a}^{2}}{{y}^{2}}}{{{b}^{2}}} \right)}dx$. Solving the integration we have, $$\begin{aligned} & v=\left[ \pi {{a}^{2}}y-\dfrac{{{a}^{2}}{{y}^{3}}}{{{b}^{2}}3} \right]_{-b}^{b} \\\ & \Rightarrow v=\left[ \pi {{a}^{2}}b-\dfrac{{{a}^{2}}{{b}^{3}}}{3{{b}^{2}}}-\left( \pi {{a}^{2}}\left( -b \right)-\dfrac{{{a}^{2}}{{\left( -b \right)}^{3}}}{{{b}^{2}}3} \right) \right] \\\ & \Rightarrow \left[ \pi {{a}^{2}}b-\dfrac{\pi {{a}^{2}}b}{3}+\pi {{a}^{2}}b-\dfrac{\pi {{a}^{2}}b}{3} \right] \\\ & \Rightarrow 2\pi {{a}^{2}}b-\dfrac{2\pi {{a}^{2}}b}{3} \\\ & \Rightarrow \dfrac{4}{3}\pi {{a}^{2}}b \\\ \end{aligned}$$. Hence volume is $\dfrac{4}{3}\pi {{a}^{2}}b$ when revolved around a minor axis. Now let us take the ratio of the volume about the major axis to the volume about the minor axis. We have $$\dfrac{\text{Volume about major axis}}{\text{Volume about minor axis}}=\dfrac{\dfrac{4}{3}\pi a{{b}^{2}}}{\dfrac{4}{3}\pi {{a}^{2}}b}=\dfrac{b}{a}$$ Hence the required ratio is b:a. **Note:** Students should keep in mind the formula of volume of solid when area is revolved about x axis and y axis. Keep in mind the formula of integration. Try to draw a diagram first for finding the required points (a,b). Take care of signs while solving the integration. Do not get confused between the major axis and the minor axis.