Question

The volume of a right circular cylinder whose height is 40cm and the circumference of its base is 66cm is:
A. $55440c{{m}^{3}}$
B. $34650c{{m}^{3}}$
C. $7720c{{m}^{3}}$
D. $13860c{{m}^{3}}$

Answer 1

Hint: Assume the radius of the base to be ‘r’ and obtain an equation in ‘r’ by using the formula “$\text{circumference=2}\pi \text{r}$ “ and given circumference =66cm.
Solve to get the value of ‘r’; then put the obtained value of ‘r’ and given value of ‘h’ in question in the formula “volume of right circular cylinder $=\pi {{r}^{2}}h$ “ to get the required volume.

Complete step-by-step answer:
We know that the volume of a right circular cylinder $=\pi {{r}^{2}}h$ .
Where r= radius of its base and h= height of the cylinder.
To calculate the volume of the cylinder, we need to know its height and radius of its base.
Height is given to be equal to 40 cm and we need to find our radius of its base.

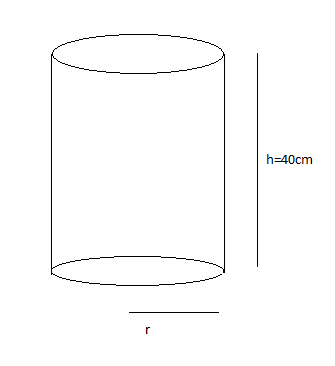
We can calculate the radius of the base by using the given information about its base. Let us assume the radius of the base =r cm.
We know circumference of a circle with radius ‘r’= $2\pi r$
According to question, circumference =66 cm
So, $2\pi r=66$ cm.
Using $\pi =\dfrac{22}{7}$ , we get
$\Rightarrow 2\times \dfrac{22}{7}\times r=66$ .
On dividing both sides of equation by ‘2’, we get,
$\Rightarrow \dfrac{22}{7}\times r=33$ .
On dividing both sides of equation by ‘11’ , we will get,
$\Rightarrow \dfrac{2}{7}\times r=3$
On multiplying both sides of equation by ‘${7}/{2}\;$ ‘, we get,
$\begin{aligned} & \Rightarrow r=\dfrac{3\times 7}{2} \\\ & \Rightarrow r=\dfrac{21}{2}cm. \\\ \end{aligned}$
Now putting h=40 cm and $r=\dfrac{21}{2}cm.$ in the formula for volume of cylinder, we will get,
Volume of cylinder $=\pi {{\left( \dfrac{21}{2} \right)}^{2}}\left( 40 \right)c{{m}^{3}}$.
Using $\pi =\dfrac{22}{7}$ , we get,
Volume of cylinder $=\dfrac{22}{7}{{\left( \dfrac{21}{2} \right)}^{2}}\left( 40 \right)c{{m}^{3}}$.
$=13860c{{m}^{3}}$ .
Hence the required volume of the given cylinder $=13860c{{m}^{3}}$ and option (D) is the correct answer.

Note: In the formula for volume, the units of radius and height should be the same. As options are given in $c{{m}^{3}}$, use all the dimensions in cm in the formula used. You don’t need to convert in SI units.