Question

The volume of a 500g sealed packet is $350c{{m}^{3}}$ . Will the packet float or sink in water if the density of water is $1gc{{m}^{-3}}$? what will be the mass of the water displaced by this packet?
(A). Sink, 500 g
(B). Sink, 350 g
(C). Float, 400 g
(D). Sink, 300 g

Answer 1

Hint: The solution to this question can be determined by comparing the densities of a packet and water and also using “Archimedes Principle”, which states that when the body is immersed fully or partially in a fluid, it experiences a upward force called the buoyant force which is equal to the weight of the fluid displaced by it.

Complete step by step answer:
This question has two parts: first finding whether the packet sinks or floats and second one how much water is displaced due to this packet.
First let us find whether packet sinks or floats:
Here they have given that – Mass of a packet = ${{m}_{p}} = 500g$
Volume of the packet –${{V}_{P}}=350c{{m}^{3}}$
Density of the water- ${{d}_{l}}=1gc{{m}^{-3}}$
We know that, density is mass per unit volume and is given by:
$d=\dfrac{m}{V}$, where d - density, m – mass of an object and V - is volume occupied by it.

So now let us calculate density of the plastic-
$\begin{aligned} & {{d}_{p}}=\dfrac{{{m}_{p}}}{{{V}_{p}}} \\\ & =\dfrac{500}{350}=1.428gc{{m}^{3}} \\\ \end{aligned}$
Here density of plastic is greater than density of water
We know that when packet is immersed in water two forces acts on it - as shown in the figure:

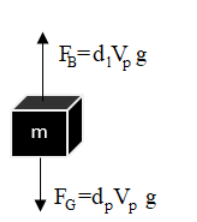
Where , ${{F}_{g}}$- Gravitational force and ${{F}_{B}}$- Buoyant force and g is acceleration due to gravity
So if the density of plastic is greater than the density of water then it implies that the gravitational force which pulls the packet downwards is greater than buoyant force which is in upward direction.
So due to the higher gravitational force packet is accelerated downwards and sinks.

Now the second part how much water is displaced due to packet:
From “Archimedes Principle” we know that, when any object is immersed in water there is an increase in the water level as much as volume occupied by an object inside the water.
Here as the packet sinks its total volume is inside water and this much of water is displaced by it. i.e.,
${{\text{V}}_{\text{packet}}}\text{= }{{\text{V}}_{\text{water displaced}}}$
Mass of this displaced water is
${{\text{M}}_{\text{water displaced}}}\text{=}{{\text{d}}_{\text{water}}}\text{ }\\!\\!\times\\!\\!\text{ }{{\text{V}}_{\text{water displaced}}}$
$\begin{aligned} & =1gc{{m}^{-3}}\times 350c{{m}^{3}} \\\ & =350g \\\ \end{aligned}$
Thus, mass of water displaced is $350g$
So the correct option is B.

Note: If the density of water is greater than the density of the packet, then the packet will float. Higher the density higher is the mass per unit volume so high dense materials will sink.