Question

The volume generated by rotating the triangle with vertices at (0,0),(3,0) and (3,3) about axis is:

Answer 1

Hint: After rotating through the axis, the slope formed will be cone. Observe radius and height of the cone to get volume.

Complete step-by-step answer:
We have given three coordinates of triangle as (0,0),(3,0) and (3,3): Let us represent these coordinates on coordinate plane:

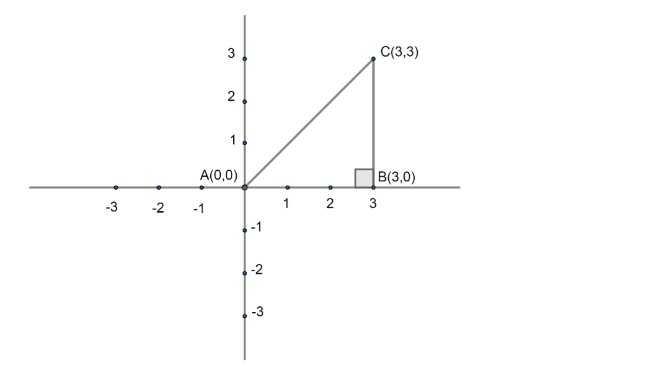
Now, by representation only, we get that the given triangle is a right angled triangle at point (3,0). We can verify it by using Pythagoras formula as
$\left( Hypotenuse \right)={{\left( Base \right)}^{2}}+{{\left( Height \right)}^{2}}$
Distance formula between two points $\left( {{x}_{1}},{{y}_{1}} \right)\And \left( {{x}_{2}},{{y}_{2}} \right)$ is
$\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Hence, from the given triangle on coordinate axis we get sides of triangle as;

& AC=\sqrt{{{\left( 3-0 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}}=\sqrt{18}=\sqrt{9\times 2} \\\ & AC=3\sqrt{2} \\\ \end{aligned}$$ And AB can be calculated as; $\begin{aligned} & AB=\sqrt{{{\left( 3-0 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}=\sqrt{9}=3 \\\ & AB=3 \\\ \end{aligned}$ For BC we can write; $\begin{aligned} & BC=\sqrt{{{\left( 3-3 \right)}^{2}}+{{\left( 0-3 \right)}^{2}}}=\sqrt{9}=3 \\\ & BC=3 \\\ \end{aligned}$ Now for using Pythagoras relation, we have three sides of triangle AB,BC and AC. As longest side of right angled triangle is hypotenuse, i.e. AC should be hypotenuse if the given triangle is the right angle. Hence, $\begin{aligned} & {{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( 3 \right)}^{2}}+{{\left( 3 \right)}^{2}}=18 \\\ & \And {{\left( AC \right)}^{2}}={{\left( 3\sqrt{2} \right)}^{2}}=18 \\\ \end{aligned}$ Therefore, ${{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( AC \right)}^{2}}$ It is proved that a given triangle is a right angled triangle. Now, we are rotating the given triangle about the axis i.e. X-axis on which base of the given triangle is lying.  We can observe that if we rotate right angle triangle about AB or X-axis, we will get a cone type structure with height 3 and diameter 6 and slant height of that cone should be $3\sqrt{2}$ from given diagram:  Now, we get height of cone=3 Slant height of cone= $3\sqrt{2}$ Radius of cone =3 As we know volume of cone is $\dfrac{1}{3}\pi {{R}^{2}}H$ Where R=radius of cone H=height of cone Therefore, volume of given cone is $\dfrac{1}{3}\times \pi \times {{\left( 3 \right)}^{2}}\times 3=9\pi uni{{t}^{3}}$ Hence, the volume of shape generated by rotating the given triangle about the axis is $9\pi uni{{t}^{3}}$. Note: One can go wrong with the rotation part and get confused between the height radius of the cone formed. One can put diameter length at the place of radius during calculation. We need to plot the given coordinates for checking the right angle. We can use Pythagoras directly. We have shown them on a coordinate plane for better understanding of the problem.