Question

The voltmeter shown in the figure reads $18\;V$ across $50\;$ ohm resistor. The resistance of the voltmeter is nearly

(A) $140\Omega$
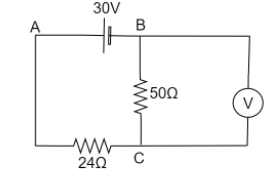
(B) $128.5\Omega$
(C) $103\Omega$
(D) $162\Omega$

Answer 1

To solve this problem, we use Kirchhoff’s Junction law to obtain the different amounts of current flowing through the resistors. This can be used to determine the amount of current flowing through the voltmeter. After this, we can use Ohm’s law to determine the resistance of the voltmeter.
Formula used:
$V = IR$

Complete step by step answer:
In the given circuit, we have the voltmeter connected in parallel with the $50\Omega$ resistor. The current originates from the positive terminal of the $30\;V$ battery and divides into two streams at the point $C$. The division of current can be determined by Kirchhoff’s current law or Kirchhoff’s junction law. Which states that at a junction, the total amount of current entering must be equal to the total amount of current leaving it.

Let current $I$ be the current coming out of the positive terminal of $30\;V$ battery, let ${I_1}$ be the current entering the $50\Omega$ resistor, and let ${I_2}$ be the current entering the voltmeter.
Now consider the junction $C$,
Here, current entering the junction= ${I_1}$
And the current leaving the junction$= {I_2} + {I_3}$
Then, according to Kirchhoff's junction law,
${I_1} = {I_2} + {I_3}$
It is given that the voltage across the $50\Omega$ resistor (or between $CB\;$ or $FE\;$ ) is $18\;V$,
Thus, the current across the $50\Omega$ resistor is-
${I_2} = \dfrac{{{V_{CB}}}}{{{R_{CB}}}}$
Putting the values,
${I_2} = \dfrac{{18}}{{50}}$
${I_2} = 0.36A$
Now, the voltage across $24\Omega$ resistor (or between $DC\;$) is,
$30 - 18 = 12V$
Thus, the current across the $24\Omega$ resistor,
${I_1} = \dfrac{{{V_{DC}}}}{{{R_{DC}}}}$
Putting the values,
${I_1} = \dfrac{{12}}{{24}}$
$\Rightarrow$ ${I_1} = 0.5A$
Putting these values at the junction $C$, we get-
$0.5 = 0.36 + {I_3}$
$\Rightarrow$ ${I_3} = 0.14A$
The current that flows across the voltmeter is ${I_3} = 0.14A$
We know that the voltage across the voltmeter is, $V = 18$
Therefore, the resistance across the voltmeter is,
$R = \dfrac{V}{{{I_3}}}$
Putting the values we have,
$R = \dfrac{{18}}{{0.14}}$
$\Rightarrow$ $R = 128.6\Omega$

Thus, option (2) is the correct answer.

Note: The points in a circuit which do not have any component other than wire have the same potential and carry the same current unless it is a resistance wire or a junction. For example, the points, $B$ and $E$ have the same potential.