Question
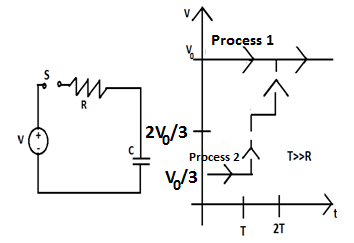
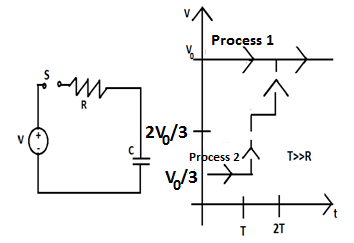
Question: The voltage is set to \[\dfrac{{{V}_{0}}}{3}\] and maintained for a charging time \[T>>RC\]. Then th...
The voltage is set to 3V0 and maintained for a charging time T>>RC. Then the voltage is raised to 32V0without discharging the capacitor and again maintained for a time T>>RC. The process is repeated one more time by raising the voltage to V0and the capacitor is charged to the same final voltage V0. In process 2, the total energy dissipated across the resistance EDis-
(A). ED=3(21CV02)
(B). ED=21CV02
(C). ED=3CV02
(D). ED=31(21CV02)
Solution
When a capacitor is being charged some energy is dissipated across the resistance. The energy stored in a capacitor is directly proportional to the square of the potential difference. The total energy dissipated is the difference of work done by the battery and the energy stored on the capacitor.
Formulas Used:
E=21CV2
ED=Wbattery−U
Complete answer:
A capacitor is a device which stores charge on it in the presence of an electric field. The capacitance is given in farad. The energy stored in a capacitor is given by-
E=21CV2
Here, E is the energy stored in a capacitor
C is it capacitance
V is the potential difference between the plates of a capacitor
When the battery does work, some of it is stored as energy in the capacitor and some of it is dissipated as heat across the resistor. In the above case, when energy of the capacitance changes due to change in its potential difference, energy is dissipated across the resistor.
Energy dissipated,ED is given by-
ED=Wbattery−U
Here,
Wbattery is the work done by the battery
Uis the energy stored in the capacitor
∴ED=21CVf2−21CVi2
VfandViare the final and initial potential drops on the capacitor respectively. Therefore, according to process 2-
