Question

The voltage drop across a forward biased diode is $0.7\,V$ In the following circuit, the voltage across the $10\Omega$ resistance in series with the diode and $20\Omega$ resistance are,

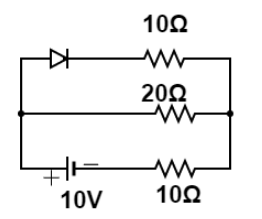
A. $0.70V,4.28V$
B. $3.58V,4.28V$
C. $5.35V,2.14V$
D $3.58V,9.3V$

Answer 1

In order to solve this question we have to understand diodes. Diodes are actually a combination of two different types of semiconductor, one is p-type and other is n-type semiconductor. Since electrons are the majority charge carrier in n-type semiconductor whereas holes are majority in p-type semiconductor.

Complete step by step answer:
So due to concentration gradient electrons move towards p side and holes move toward n side, hence a region of immobile ions created around junction is known as depletion region in which electric field is from n side to p side. So when diode is forward bias means p side connected to positive side of voltage an n to negative, Electric field starts building from p side to n side and eventually current starts to flow inside diode.

So to solve this circuit, we know an ideal diode in forward bias behaves as a closed circuit so it is replaced by a wire while a non-ideal diode is replaced by some voltage difference generated across it. So in this circuit diode is replaced by $0.7V$ battery and let total current be “i” from $10V$ battery distributed in circuit as shown

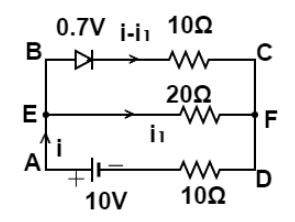
So applying Kirchhoff’s law in loop ABCDA we get,
$0.7 + 10(i - {i_1}) + 10i - 10 = 0$
$\Rightarrow 20i - 10{i_1} = 9.3$
$\Rightarrow 2i - i{{\kern 1pt} _1} = 0.93 \to (i)$
Applying Kirchhoff’s law in loop AEFDA we get,
$20{i_1} + 10i - 10 = 0$
$\Rightarrow 20{i_1} + 10i = 10$
$\Rightarrow i + 2{i_1} = 1 \to (ii)$
Now, Multiply first equation by two and add second equation as $(i) \times 2 + (ii)$ we get
$5i = 2.86$
$\Rightarrow i = 0.572A$

Putting the value of “i” in equation (i). We get,
${i_1} = 2(0.572) - 0.93$
$\Rightarrow {i_1} = 0.214A$
So Voltage drop across $10\Omega$ resistance in series with diode is,
${V_1} = 10 \times (i - {i_1})$
Putting values we get,
${V_1} = 10 \times (0.572 - 0.214)$
$\Rightarrow {V_1} = 3.58V$
Similarly voltage across $20\Omega$ resistance is, ${V_2} = 20{i_i}$
Putting values we get, ${V_2} = 20 \times 0.214$
$\therefore {V_2} = 4.28V$

So, the correct option is B.

Note: It should be remembered that Kirchhoff’s law is conservation law. First law states that there should not be accumulation of charges at the junction so at the junction current remains continuous and this is supported by the equation of continuity. Second law states that total voltage drop across the loop is zero so as to verify tellangan’s theorem of power dissipation.