Question

The vibrations of four air columns are represented in the figure. The ratio of frequencies np : nq : nr : ns is

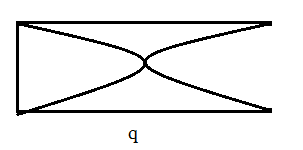
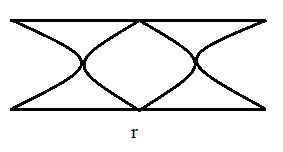
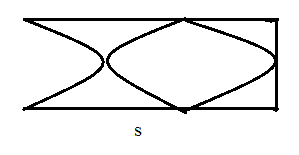
A. 12 : 6 : 3 : 5
B. 1 : 2 : 4 : 3
C. 4 : 2 : 3 : 1
D. 6 : 2 : 3 : 4

Answer 1

In the case of the closed end air column, the wavelength to be considered will be 4 times the length of the column, whereas, in the case of the open end air column, the wavelength to be considered will be 2 times the length of the column, while calculating the frequencies.

Formula used:
$n=\dfrac{v}{4l}$
$n=\dfrac{v}{2l}$

Complete step by step answer:
The air column p represents the fundamental closed end.
Thus the frequency of the air column p is given as,
${{n}_{p}}=\dfrac{v}{4l}$

The air column q represents the fundamental open end.
Thus the frequency of the air column q is given as,
${{n}_{q}}=\dfrac{v}{2l}$

The air column r represents the second overtone open end.
Thus the frequency of the air column r is given as,

& {{n}_{r}}=\dfrac{2v}{2l} \\\ & {{n}_{r}}=\dfrac{v}{l} \\\ \end{aligned}$$ The air column s represents the second overtone closed end. Thus the frequency of the air column s is given as, $${{n}_{s}}=\dfrac{3v}{4l}$$ The ratio of the frequencies of the air columns p, q, r and s is given as follows: $${{n}_{p}}:{{n}_{q}}:{{n}_{r}}:{{n}_{s}}=\dfrac{1}{4}:\dfrac{1}{2}:1:\dfrac{3}{4}$$ Multiply by 4 to take the LCM. Therefore, the ratio of the frequencies is, $${{n}_{p}}:{{n}_{q}}:{{n}_{r}}:{{n}_{s}}=1:2:4:3$$ As, the ratio of frequencies np : nq : nr : ns of four air columns is 1 : 2 : 4 : 3, thus option (B) 1 : 2 : 4 : 3 is correct. **Note:** The things to be on your finger-tips for further information on solving these types of problems are: The frequencies should be calculated considering open end and the closed end concepts.