Question

The vessels A and B of equal volume and weight are immersed in water to depth h. The vessel A has an opening at the bottom through which water can enter. If the work done in immersing A and B are $W_A$​ and $W_B$ ​respectively, then

& A){{W}_{A}}={{W}_{B}} \\\ & B){{W}_{A}}<{{W}_{B}} \\\ & C){{W}_{A}}>{{W}_{B}} \\\ & D){{W}_{A}}\ge {{W}_{B}} \\\ \end{aligned}$$

Answer 1

We will apply Archimedes principle here because both the vessels are immersed in liquid. So according to this upthrust acts on it and its magnitude will depend on the volume of immersed part and also on the density of the liquid. When an opening is immersed in part then upthrust on that part is removed.

Complete answer:
Two vessels A and B are of equal volume and equal weight is immersed in water.
Let us assume the Weight of both vessels is W.
Let us assume upthrust acting is represented by U.
Weight always acts in downward direction so in this figure they are acting in downwards direction.
According to the question, both vessels are immersed to height h in the water.
So , according to Archimedes Principle, when any object is partially or wholly immersed in the liquid then buoyant force or upthrust acts on that body. So here on both the vessel buoyancy force will act in upwards direction.

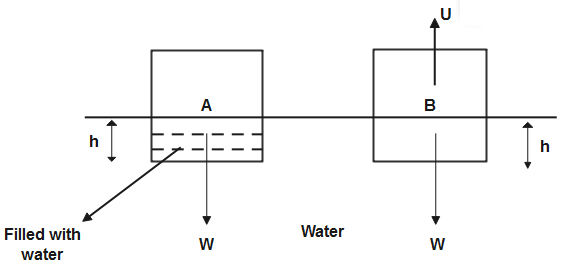
But according to question Vessel A has some opening through which water can enter so immersed part of vessel A is completely filled with water. So the immersed part of Vessel A is not acted by upthrust because it is immersed in water. So only upthrust will work on the immersed part of vessel B.
Now if we try to immersed both the vessel then for vessel A no force is acting in upwards direction to acts against work done in immersing the vessel A while in vessel B upthrust is acting in upwards direction to act against work done in immersing the vessel B. So more Work is require to be done on vessel B in comparison to vessel A.
Work done in immersing Vessel A is less than Work done in immersing Vessel B.
So mathematically we can write ,
${{W}_{A}}<{{W}_{B}}$

So option B is correct.

Note:
When a certain liquid is held in static equilibrium against boundary surfaces, the forces exert by liquid always perpendicular to the surface in contact. This is so because a liquid at rest cannot resist any tangential force. When a fluid (either liquid or gas) is at rest, it exerts a force perpendicular to any surface in contact with it, such as a container wall or a body immersed in the fluid.