Question
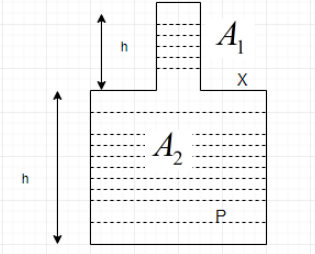
Question: The vessel shown in the figure has two sections of areas of cross section \({{A}_{1}}\) and \({{A}_{...
The vessel shown in the figure has two sections of areas of cross section A1 and A2. A liquid of density ρ fills both the sections, up to a height h in each. Neglect atmospheric pressure.
(A) The pressure at the base of the vessel is 2ρgh
(B) The force exerted by the liquid on the base of the vessel is 2ρghA2
(C) The weight of the liquid is ⟨2hρgA2
(D) The walls of the vessel at the level X exert a downward force ρgh(A2−A1) on the liquid.
Solution
The liquid in both the columns is the same, so we do not have to worry about mixing and all. Also, the height of both the columns are the same. We know that liquid exerts pressure and that can be hurriedly found using Pascal’s law of pressure. Also, liquid has weight and we can find the force of gravity using mass, density and the volume.
Complete step by step answer:
This question can have multiple correct answers. Let us check all the options given one by one.We know that the same liquid is filled, so the total height of the water column comes out to be h+h=2h. So, the pressure exerted at the bottom comes out to be ρg(2h)=2ρgh. So, option A is correct.
We know from Pascal’s law of pressure, pressure is given by P=AF, so force becomes F=PA. Now the area of the column at the base is A2. So, force at the bottom becomesPA2=2ρghA2. So, option B is also correct.
Now let us talk about the weight, the weight will be exerted by the water in the column at the top and the column at the bottom and it is clear that the net weight of the liquid will be greater that 2ρghA2 which the weight of the water in the column at the bottom.So, option C is also correct.Now talking about option D, ΔF=ρghA2−ρghA1=ρgh(A2−A1). So, option D is also correct.
Hence all the given options are correct.
Note: Pascal’s law of pressure states that if a pressure is exerted at any point in a liquid then it is distributed equally in all the direction.The ability of fluids to transmit pressure is the key point which holds the Pascal’s law. This law has many applications in our everyday lives. The working of hydraulic lift, hydraulic jack, hydraulic press and forced amplification is used in the braking system of most cars is based on Pascal’s law.
