Question

The vertices of the triangle are P(2,1), Q(4,-1) and R(3,2). If through P and R lines parallel to opposite sides are drawn to intersect in S, then what is the area of PQRS?
(a) 6
(b) 4
(c) 8
(d) 12

Answer 1

- Hint: First of all we will construct the triangle as told in the question. Then we will find the point of intersection of the newly drawn line. Then we use the midpoint formula to get the final answer.

Complete step-by-step solution -

The formula needed for this question is the area of the triangle given three points. I am going to explain a concept here, which is true about any triangle, and this concept is used here.

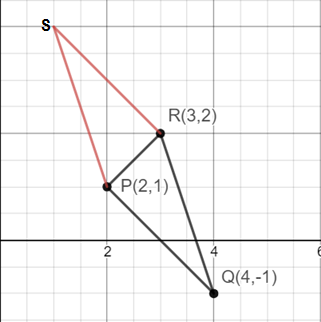
You can see the triangle in black lines, already given in the question. Now when we draw lines through P and R lines parallel to opposite sides they intersect at one point which we named S according to the question.
Now in any triangle PQR if this procedure is done, we always get a parallelogram PQRS no matter what we do and how we do.
Also, as you can see in the figure, the triangle is always the half of parallelogram in terms of area.
So, to calculate the area of the parallelogram we can calculate the area of the triangle and then multiply it by 2.
Let us do this.
Area of parallelogram = 2$\times$ area of triangle
We will find the area of triangle using matrix, so we get

{{x}_{1}} & {{y}_{1}} & 1 \\\ {{x}_{2}} & {{y}_{2}} & 1 \\\ {{x}_{3}} & {{y}_{3}} & 1 \\\ \end{matrix} \right)$$ Here $$\left( {{x}_{1}},\text{ }{{y}_{1}} \right)=\left( 2,\text{ }1 \right),\text{ }\left( {{x}_{2}},\text{ }{{y}_{2}} \right)=\left( 4,\text{ }-1 \right),\left( {{x}_{3}},\text{ }{{y}_{3}} \right)=\left( 3,2 \right)$$, so we get $$ar(PQRS)=\left( \begin{matrix} 2 & 1 & 1 \\\ 4 & -1 & 1 \\\ 3 & 2 & 1 \\\ \end{matrix} \right)$$ $$\begin{aligned} & ar(PQRS)=\left( \begin{matrix} 2 & 1 & 1 \\\ 4 & -1 & 1 \\\ 3 & 2 & 1 \\\ \end{matrix} \right) \\\ & ar(PQRS)=2((-1)(1)-(2)(1))-1((4)(1)-(3)(1))+1((4)(2)-(3)(-1)) \\\ & ar(PQRS)=2(-1-2)-(4-3)+(8+3) \\\ & ar(PQRS)=2(-3)-1+11 \\\ & ar(PQRS)=-6-1+11=4 \\\ \end{aligned}$$ Thus, the area of the quadrilateral PQRS is 4 sq. units. _Therefore, option(b) is correct._ Note: While in exam, drawing rough figures is very important. However, be sure that you draw them as neat and correct as possible. If you draw the diagram haphazardly, you might not notice that the triangle after some construction looks like a parallelogram and you might take up some other method to find out the area and waste a lot of time.