Question

The vertices of the triangle are $\left( {6,0} \right)$ , $\left( {0,6} \right)$ and $\left( {6,6} \right)$ . The distance between its circumcenter and centroid is
A.$2$
B.$\sqrt 2$
C.$1$
D$2\sqrt 2$

Answer 1

Hint : In the question related to the vertices of a triangle , always draw a figure for better understanding . The two of its vertices will act as the coordinates of the diameter of the circumcircle inscribed . For finding the centroid we have the formula for it .

Complete step-by-step answer :
Given : $\left( {6,0} \right)$ , $\left( {0,6} \right)$ and $\left( {6,6} \right)$ . We draw the triangle using these vertices

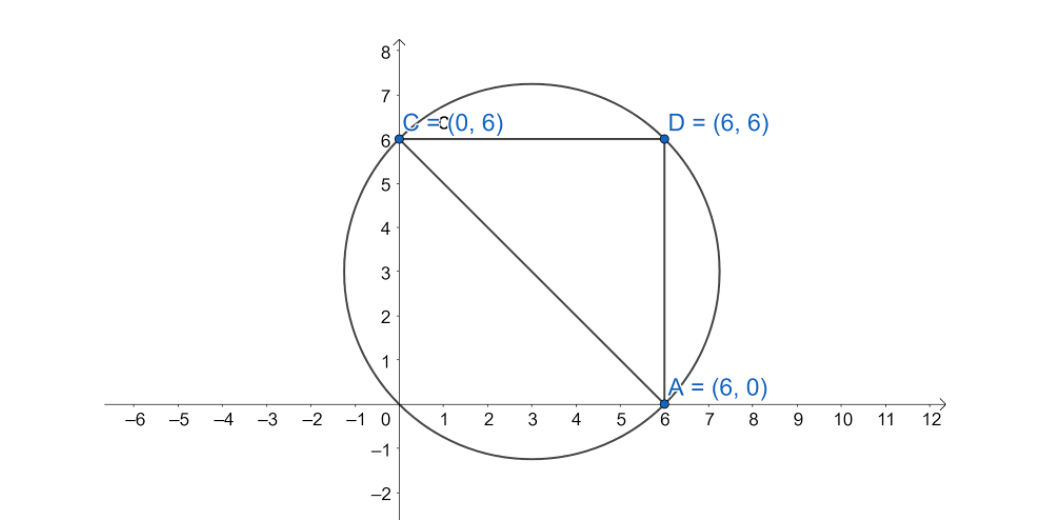
From the figure we get that the coordinates $\left( {6,0} \right)$ and $\left( {0,6} \right)$ will act as the diameter of the circle .
Therefore , the circumcenter of the circle will be $= \left( {\dfrac{{0 + 6}}{2},\dfrac{{6 + 0}}{2}} \right)$ , on solving we get
$= \left( {3,3} \right)$ .
You can also understand that we are finding the midpoint of the diameter which will be the circumcenter .
Now , for the centroid we use the formula $= \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$ , on putting the values we get ,
$= \left( {\dfrac{{0 + 6 + 6}}{3},\dfrac{{6 + 0 + 6}}{3}} \right)$ , on solving we get ,
$= \left( {4,4} \right)$ .
This is the coordinates for centroid .
Now , for the distance between circumcenter and centroid we will use distance formula $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$ .
On putting the values we get ,
$= \sqrt {{{\left( {4 - 3} \right)}^2} + {{\left( {4 - 3} \right)}^2}}$
$= \sqrt {{1^2} + {1^2}}$ , on solving we get
$= \sqrt 2$
Therefore , option (B) is the correct answer .
So, the correct answer is “Option B”.

Note : The centroid of a triangle is the intersection of the three medians of the triangle ( each median connecting a vertex with the midpoint of the opposite side ) . The circumcenter is the center point of the circumcircle drawn around a polygon. This means that the perpendicular bisectors of the triangle are concurrent (i.e. meeting at one point) .