Solveeit Logo
Login

Question

Question: The vertices of an equilateral triangle are \(\left( 3,2 \right),\left( 3,-2 \right),\left( 0,h \rig...

The vertices of an equilateral triangle are (3,2),(3,−2),(0,h)\left( 3,2 \right),\left( 3,-2 \right),\left( 0,h \right) then h=h=
A. 3 B. 2±27 C. 2-27 D. 2+27 \begin{aligned} & \text{A}\text{. }\sqrt{3} \\\ & \text{B}\text{. }\sqrt{2}\pm \sqrt{27} \\\ & \text{C}\text{. 2-}\sqrt{27} \\\ & \text{D}\text{. 2+}\sqrt{27} \\\ \end{aligned}

Explanation

Solution

First we draw a diagram of equilateral triangle and assume that three vertices of triangle are(3,2),(3,−2),(0,h)\left( 3,2 \right),\left( 3,-2 \right),\left( 0,h \right). Then, we use the distance formula to calculate the length of the side of a triangle. Now, we know that the equilateral triangle has all sides equal so we use the concept to obtain the answer.

Complete step by step answer:
The distance formula used is (x2−x1)2+(y2−y1)2\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
Where, x2,x1,y2,y1{{x}_{2}},{{x}_{1}},{{y}_{2}},{{y}_{1}} are coordinates of vertices.
We have given that (3,2),(3,−2),(0,h)\left( 3,2 \right),\left( 3,-2 \right),\left( 0,h \right) are vertices of an equilateral triangle.
We have to find the value of hh.
Let us assume ABCABC is an equilateral triangle and A(3,2),B(3,−2),C(0,h)A\left( 3,2 \right),B\left( 3,-2 \right),C\left( 0,h \right) are three vertices.

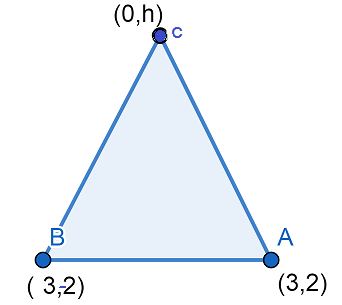
Now, we know that the length of all sides of an equilateral tringle is equal. AB=BC=ACAB=BC=AC
Also, length of side is calculated by finding the distance between two vertices. The distance is calculated by using the formula (x2−x1)2+(y2−y1)2\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
Where, x2,x1,y2,y1{{x}_{2}},{{x}_{1}},{{y}_{2}},{{y}_{1}} are coordinates of vertices.
Now, the length of AB=(x2−x1)2+(y2−y1)2AB=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
⇒AB=(−3−3)2+(2−2)2 ⇒AB=(−6)2+(0)2 ⇒AB=6 \begin{aligned} & \Rightarrow AB=\sqrt{{{\left( -3-3 \right)}^{2}}+{{\left( 2-2 \right)}^{2}}} \\\ & \Rightarrow AB=\sqrt{{{\left( -6 \right)}^{2}}+{{\left( 0 \right)}^{2}}} \\\ & \Rightarrow AB=6 \\\ \end{aligned}
Now, the length of BC=(x2−x1)2+(y2−y1)2BC=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
⇒BC=(0−(−3))2+(h−2)2 ⇒BC=(3)2+(h−2)2 ⇒BC=9+(h−2)2 \begin{aligned} & \Rightarrow BC=\sqrt{{{\left( 0-\left( -3 \right) \right)}^{2}}+{{\left( h-2 \right)}^{2}}} \\\ & \Rightarrow BC=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( h-2 \right)}^{2}}} \\\ & \Rightarrow BC=\sqrt{9+{{\left( h-2 \right)}^{2}}} \\\ \end{aligned}
Now, the length of CA=(x2−x1)2+(y2−y1)2CA=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
⇒CA=(3−0)2+(2−h)2 ⇒CA=(3)2+(2−h)2 ⇒CA=9+(2−h)2 \begin{aligned} & \Rightarrow CA=\sqrt{{{\left( 3-0 \right)}^{2}}+{{\left( 2-h \right)}^{2}}} \\\ & \Rightarrow CA=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( 2-h \right)}^{2}}} \\\ & \Rightarrow CA=\sqrt{9+{{\left( 2-h \right)}^{2}}} \\\ \end{aligned}
Now, we know that AB=BC=ACAB=BC=AC, so 9+(h−2)2=9+(2−h)2=6\sqrt{9+{{\left( h-2 \right)}^{2}}}=\sqrt{9+{{\left( 2-h \right)}^{2}}}=6
Or 9+(h−2)2=6\sqrt{9+{{\left( h-2 \right)}^{2}}}=6 and 9+(2−h)2=6\sqrt{9+{{\left( 2-h \right)}^{2}}}=6
Let us first consider 9+(h−2)2=6\sqrt{9+{{\left( h-2 \right)}^{2}}}=6
Now, simplifying further, we get

& \sqrt{9+{{h}^{2}}+4-4h}=6 \\\ & \sqrt{{{h}^{2}}-4h+13}=6 \\\ & {{h}^{2}}-4h+13=36 \\\ & {{h}^{2}}-4h=36-13 \\\ & {{h}^{2}}-4h=23 \\\ & {{h}^{2}}-4h-23=0 \\\ \end{aligned}$$ Now, let us solve the above equation by using the formula $\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ Now, we have $$\begin{aligned} & \Rightarrow h=\dfrac{-\left( -4 \right)\pm \sqrt{{{\left( -4 \right)}^{2}}-4\times 1\times \left( -23 \right)}}{2\times 1} \\\ & \Rightarrow h=\dfrac{4\pm \sqrt{16+92}}{2} \\\ & \Rightarrow h=\dfrac{4\pm \sqrt{108}}{2} \\\ & \Rightarrow h=\dfrac{4\pm 2\sqrt{27}}{2} \\\ & \Rightarrow h=\dfrac{2\left( 2\pm \sqrt{27} \right)}{2} \\\ & \Rightarrow h=2\pm \sqrt{27} \\\ \end{aligned}$$ So, the value of $h$ is $2\pm \sqrt{27}$. Now, since it is given in the question that h < 0, we have to choose the value of h as $2-\sqrt{27}$ . **So, the correct answer is “Option A”.** **Note:** The key concept is to use the property of equilateral triangle to solve the question and use the distance formula to calculate the lengths of the sides of an equilateral triangle. The equation ${{h}^{2}}+4h-3=0$ can be solved using the factorization method to find the value of $h$.