Question

The vertices of a triangle OBC are $( 0,0 ) , ( - 3 , - 1 )$ and $( - 1 , - 3 )$respectively. Then the equation of line parallel to BC which is at $\frac { 1 } { 2 }$unit distant from origin and cuts OB and OC, is.

• A. $2 x + 2 y + \sqrt { 2 } = 0$
• B. $2 x + 2 y - \sqrt { 2 } = 0$
• C. $2 x - 2 y + \sqrt { 2 } = 0$
• D. None of these

Answer 1

Answer: (A)

$2 x + 2 y + \sqrt { 2 } = 0$

Answer 2

Gradient of $B C = - 1$ and its equation is $x + y + 4 = 0$. Therefore the equation of line parallel to $B C$is $x + y + \lambda = 0$.Also it is $\frac { 1 } { 2 }$unit distant from origin. Thus

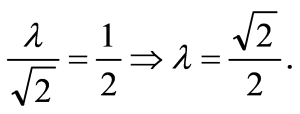
Hence the required equation of line is $2 x + 2 y + \sqrt { 2 } = 0$.