Question

The vertices of a triangle are A $\left( {p,p\tan \alpha } \right)$, B $\left( {q,q\tan \beta } \right)$, C $\left( {r,r\tan \gamma } \right)$ respectively. If the circumcentre ‘${\text{O}}$’ of the triangle ABC is at the origin and H $\left( {\bar x,\bar y} \right)$ be its orthocenter, then show that: $\dfrac{{\bar x}}{{\bar y}} = \dfrac{{\cos \alpha + \cos \beta + \cos \gamma }}{{\sin \alpha + \sin \beta + \sin \gamma }}$.

Answer 1

The given problem revolves around the concepts of proving the equation of geometry-type solutions. As a result, to prove such equation first finding the value of unknown variable i.e. here ‘$p$’ with the help of circle equation ${x^2} + {y^2} = {r^2}$ by substituting the respective x and y variable of the given vertices. Then, finding the centroid of the triangle ABC by the formula ${\text{G}} \equiv \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$. Hence, using the slope condition that is $y = mx$ and $Slope{\text{ }}of{\text{ }}OG = Slope{\text{ }}of{\text{ }}OH$ respectively, the desired proof is obtained.

Complete answer:
Since, we have given that
A, B and C are the respective vertices of the triangle ABC that is,
$A \equiv \left( {p,p\tan \alpha } \right)$, … (i)
$B \equiv \left( {q,q\tan \beta } \right)$, and … (ii)
$C \equiv \left( {r,r\tan \gamma } \right)$ respectively. … (iii)
Since,
By the given conditions that ‘${\text{O}}$’ is the circumcentre that is the centre of the circle included or excluded in the given triangle ABC,

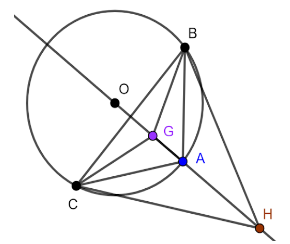
Therefore,
The given vertices of the triangle ‘$\vartriangle ABC$’ implies the equation of the circle that is ${x^2} + {y^2} = {r^2}$,
Hence, by substituting the vertices in the above circle equation, we get
[Considering $A \equiv \left( {p,p\tan \alpha } \right)$ ]
${p^2} + {p^2}{\tan ^2}\alpha = {R^2}$
Solving the equation mathematically, we get
${p^2}\left( {1 + {{\tan }^2}\alpha } \right) = {R^2}$
Since, we know that the trigonometric identity for/is “$1 + {\tan ^2}\theta = {\sec ^2}\theta$”, the equation becomes
${p^2}{\sec ^2}\alpha = {R^2}$
$p\sec \alpha = R$ … ($\because$ Taking square roots)
Hence, the value for ‘$p$’ becomes,
$p = R\cos \alpha$ … (iv)
Where, $\dfrac{1}{{\cos \alpha }} = \sec \alpha$!
Hence, equation/vertices of ‘${\text{A}}$’ i.e. in (i) becomes (that is substituting the value of ‘$p$’), we get
$A \equiv \left( {R\cos \alpha ,R\cos \alpha \tan \alpha } \right)$
… ($\because$ Where, ‘${\text{R}}$’ is the radius of the same circle i.e. same for the remaining two vertices respectively)
Since, we know that the trigonometric identity for/is ‘$\dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta$’, the equation becomes
$\Rightarrow A \equiv \left( {R\cos \alpha ,R\sin \alpha } \right)$ … (v)
Similarly,
For the other two vertices of the $\vartriangle ABC$ that is $B \equiv \left( {q,q\tan \beta } \right)$ and $C \equiv \left( {r,r\tan \gamma } \right)$ respectively, we get
$p = R\cos \beta$ … (vi)
And, $p = R\cos \gamma$ … (vii)
Hence, the vertices ‘$B$’ and ‘$C$’ (by substituting these values for ‘$p$’ particularly) is
$\Rightarrow B \equiv \left( {R\cos \beta ,R\sin \beta } \right)$ … (viii)
And,
$\Rightarrow C \equiv \left( {R\cos \gamma ,R\sin \gamma } \right)$ … (ix)
Now,
As a result, to prove the equation
Considering the ‘${\text{G}}$’ as the centroid of the $\vartriangle ABC$,
Hence, by using its definition/formulae that is ${\text{G}} \equiv \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$, we get
[From equations (v), (viii) and (ix)]
$G = \left( {\dfrac{{R\cos \alpha + R\cos \beta + R\cos \gamma }}{3},\dfrac{{R\sin \alpha + R\sin \beta + R\sin \gamma }}{3}} \right)$ … (x)
Given that: Circumcentre ‘${\text{O}}$’ is at origin that is $O \equiv \left( {0,0} \right)$ and orthocentre ‘${\text{H}}$’ is $\left( {\bar x,\bar y} \right)$ respectively. … (xi)
From figure it implies that,
Points ‘${\text{O}}$’, ‘${\text{G}}$’ and ‘${\text{H}}$’ are collinear that lie on the same line.
Hence, by using the slope condition i.e. $y = mx$
Hence, $m = \dfrac{y}{x}$
$\Rightarrow Slope{\text{ }}of{\text{ }}OG = Slope{\text{ }}of{\text{ }}OH$
Mathematically, equation can be written as
$\bar g - \bar o = \bar h - \bar o$
Substituting the values from equations (x) and (xi), we get
$\Rightarrow \left( {\dfrac{{\dfrac{{R\sin \alpha + R\sin \beta + R\sin \gamma }}{3}}}{{\dfrac{{R\cos \alpha + R\cos \beta + R\cos \gamma }}{3}}}} \right) - 0 = \dfrac{{\bar y}}{{\bar x}} - 0$
$\Rightarrow \dfrac{{R\sin \alpha + R\sin \beta + R\sin \gamma }}{{R\cos \alpha + R\cos \beta + R\cos \gamma }} = \dfrac{{\bar y}}{{\bar x}}$
Dividing by radius ‘${\text{R}}$’ as the whole equation i.e. in R.H.S. contains ‘${\text{R}}$’, we get
$\Rightarrow \dfrac{{R\left( {\sin \alpha + \sin \beta + \sin \gamma } \right)}}{{R\left( {\cos \alpha + \cos \beta + \cos \gamma } \right)}} = \dfrac{{\bar y}}{{\bar x}}$
$\Rightarrow \dfrac{{\sin \alpha + \sin \beta + \sin \gamma }}{{\cos \alpha + \cos \beta + \cos \gamma }} = \dfrac{{\bar y}}{{\bar x}}$
As a result, transposing or taking the reciprocal of the equation, we get
$\Rightarrow \dfrac{{\cos \alpha + \cos \beta + \cos \gamma }}{{\sin \alpha + \sin \beta + \sin \gamma }} = \dfrac{{\bar x}}{{\bar y}}$, or
$\Rightarrow \dfrac{{\bar x}}{{\bar y}} = \dfrac{{\cos \alpha + \cos \beta + \cos \gamma }}{{\sin \alpha + \sin \beta + \sin \gamma }}$
$\therefore \Rightarrow$Hence, proved!

Note:
Remember that by the definitions of ‘Orthocentre’, ‘Circumcentre’ and ‘Centroid’ it lies on the same line that is said ‘Collinear’ property for the respective parameters given, hence the slope condition exists (must applicable) that is $Slope{\text{ }}of{\text{ }}OG = Slope{\text{ }}of{\text{ }}OH$ , so as to be sure of the final answer.