Solveeit Logo
Login

Question

Question: The vertices of a triangle are \(A\left( -1,7 \right)B\left( 5,1 \right)\) and \(C\left( 1,4 \right)...

The vertices of a triangle are A(−1,7)B(5,1)A\left( -1,7 \right)B\left( 5,1 \right) and C(1,4)C\left( 1,4 \right). The equation of the bisector of is?

  1. x−7y+2=0x-7y+2=0
  2. x+y−6=0x+y-6=0
  3. x+2y−7=0x+2y-7=0
  4. 116x−39y=157116x-39y=157
Explanation

Solution

Here we have to find the equation of the angle bisector of angle ABC. For that, we will first draw the triangle and mark the given points. We will equate the ratio at which the angle bisector divides the opposite side of the triangle and the ratio of length of two other sides of the triangle. From there, we will find the rate at which the angle bisector divides the opposite side of the triangle. Then we will use the section formula to find the other point of the angle bisector and we will find the equation of the angle bisector using these two points.

Complete step by step solution:
Let’s draw the triangle and mark the given points. Let the point at which the bisector of the angle ABC intersects the side AC be point D.

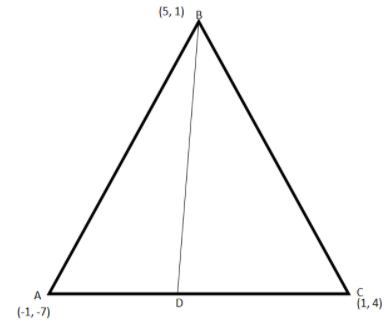
Let’s find the length of AB and BC using the distance formula.
Length of the side AB =Distance of the point (−1,−7)(-1,-7)from (5,1)(5,1) =[(5−(−1))2+(1−(−7))2]=\sqrt{\left[ {{\left( 5-(-1) \right)}^{2}}+{{\left( 1-\left( -7 \right) \right)}^{2}} \right]}
We will subtract -1 from 5 and -7 from 1 and then we will take the square of it and then square root.
Distance of the point (−1,−7)(-1,-7)from (5,1)(5,1) =10=10
Length of the side BC =Distance of the point (1,4)(1,4)from (5,1)(5,1) =[(5−1)2+(1−4)2]=\sqrt{\left[ {{\left( 5-1 \right)}^{2}}+{{\left( 1-4 \right)}^{2}} \right]}
We will subtract 1 from 5 and 4 from 1 and then we will take the square of it and then square root.
Distance of the point (1,4)(1,4)from (5,1)(5,1) =5=5
Since BD is the required bisector of angle ABC. Therefore, the ratio of length BA & BC are equal to the ratio of length DA & CD.
CD:DA=BC:BACD:DA=BC:BA
Putting the value of AB and BC, we get
CD:DA=5:10=1:2CD:DA=5:10=1:2
Since, we got the ratio, so we can easily find the value of point D using the section formula.
∴D=(2−13,−7+83) D=(13,13) \begin{aligned} & \therefore D=\left( \dfrac{2-1}{3},\dfrac{-7+8}{3} \right) \\\ & D=\left( \dfrac{1}{3},\dfrac{1}{3} \right) \\\ \end{aligned}
Since the point B is (5,1)\left( 5,1 \right) and of D is (13,13)\left( \dfrac{1}{3},\dfrac{1}{3} \right). So we can find the equation of BD now.
Equation line BD y−1=1−135−13(x−5)y-1=\dfrac{1-\dfrac{1}{3}}{5-\dfrac{1}{3}}\left( x-5 \right)
On further simplification, we get
y−1=17(x−5) x−7y+2=0 \begin{aligned} & y-1=\dfrac{1}{7}\left( x-5 \right) \\\ & x-7y+2=0 \\\ \end{aligned}
Therefore, the equation of the bisector of angle ABC is x−7y+2=0x-7y+2=0

Thus, the correct option is A.

Note:
The formula which we have used here for finding the distance between the two points is in two dimensional.
The distance formula for three dimensional is different.
Say we have to find the distance between the points (x1,y1,z1)({{x}_{1}},{{y}_{1}},{{z}_{1}}) and (x2,y2,z2)({{x}_{2}},{{y}_{2}},{{z}_{2}})
So the distance between these two points is
[(x2−x1)2+(y2−y1)2+(z2−z1)2]\sqrt{\left[ {{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}} \right]}