Question

The vertices of a hyperbola are at (0, 0) and (10, 0) and one of its focus is at (18, 0). The possible equation of hyperbola is
$\left( a \right)\dfrac{{{x^2}}}{{25}} - \dfrac{{{y^2}}}{{144}} = 1$
$\left( b \right)\dfrac{{{{\left( {x - 5} \right)}^2}}}{{25}} - \dfrac{{{y^2}}}{{144}} = 1$
$\left( c \right)\dfrac{{{x^2}}}{{25}} - \dfrac{{{{\left( {y - 5} \right)}^2}}}{{144}} = 1$
$\left( d \right)\dfrac{{{{\left( {x - 5} \right)}^2}}}{{25}} - \dfrac{{{{\left( {y - 5} \right)}^2}}}{{144}} = 1$

Answer 1

Hint – In this particular question use the concept that the center of the hyperbola is at midpoint of the line joining the two vertices of the hyperbola and the distance between the vertices is the length of the major axis i.e. 2a, and use that the coordinates of the focus from the center is at (ae, 0), where e is the eccentricity, so use these concepts to reach the solution of the equation.

Complete step-by-step answer:
__
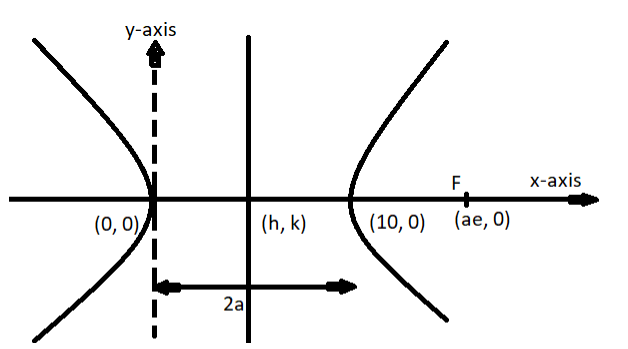
Given data:
Vertices of a hyperbola are at (0, 0) and (10, 0).
One focus of the hyperbola is at (18, 0)
As we all know that the general equation of the hyperbola is given as,
$\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} - \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$, where (h, k) is the center of the hyperbola and a, and b are the length of semi major and semi minor axis of the hyperbola.
Now as we know that the center of the hyperbola is at the midpoint of the line joining the two vertices of the hyperbola.
Let the center be (h, k)
Let, first vertex = $\left( {{x_1},{y_1}} \right) = \left( {0,0} \right)$
And second vertex = $\left( {{x_2},{y_2}} \right) = \left( {10,0} \right)$
So according to midpoint theorem the coordinates of midpoint is,
$\Rightarrow \left( {h,k} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
Now substitute the values we have,
$\Rightarrow \left( {h,k} \right) = \left( {\dfrac{{0 + 10}}{2},\dfrac{{0 + 0}}{2}} \right) = \left( {5,0} \right)$
So the center of the hyperbola is (5, 0)
Therefore, h = 5 and k = 0.
Now as we all know that the distance between the vertices is the length of the major axis i.e. 2a.
As the vertex is at (0, 0) and (10, 0), so the distance between the vertices is 10.
Therefore, 2a = 10
Therefore, a = 5.
Now it is given that one of its focus is at (18, 0).
So the distance of the focus from the center (5, 0) is
Distance of focus = 18 – 5 = 13
Now the coordinates of the focus from the center is at (ae, 0), where e is the eccentricity.
Therefore, ae = 13,
$\Rightarrow e = \dfrac{{13}}{5}$
Now as we all know that in hyperbola the relation between a, b and e is
$\Rightarrow {b^2} = {a^2}\left( {{e^2} - 1} \right)$
Now substitute the values we have,
$\Rightarrow {b^2} = {5^2}\left( {{{\left( {\dfrac{{13}}{5}} \right)}^2} - 1} \right) = {13^2} - {5^2} = 169 - 25 = 144$
So the equation of the hyperbola becomes,
$\Rightarrow \dfrac{{{{\left( {x - 5} \right)}^2}}}{{25}} - \dfrac{{{{\left( {y - 0} \right)}^2}}}{{144}} = 1$
$\Rightarrow \dfrac{{{{\left( {x - 5} \right)}^2}}}{{25}} - \dfrac{{{y^2}}}{{144}} = 1$
So this is the required equation of the hyperbola.
Hence option (b) is the correct answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall that the general equation of the hyperbola is given as, $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} - \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$, where (h, k) is the center of the hyperbola and a, and b are the length of semi major and semi minor axis of the hyperbola and in hyperbola the relation between a, b and e is ${b^2} = {a^2}\left( {{e^2} - 1} \right)$.