Solveeit Logo
Login

Question

Question: The vertices of a \(\Delta ABC\) are \(A\left( -5,7 \right)\), \(B\left( -4,-5 \right)\) and \(C\lef...

The vertices of a ΔABC\Delta ABC are A(−5,7)A\left( -5,7 \right), B(−4,−5)B\left( -4,-5 \right) and C(4,5)C\left( 4,5 \right). Find the slopes of the altitudes of the triangle.

Explanation

Solution

The altitude in a triangle is defined as the line passing through a vertex and perpendicular to the side opposite to the vertex. Therefore, for the given triangle ABC, we can let the altitudes as AP, BQ, and CR. Using the relation m=y2−y1x2−x1m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}, we can determine the slopes of all the three sides, and since altitudes are perpendicular to them, using the relation m1m2=−1{{m}_{1}}{{m}_{2}}=-1 we can determine the slopes of all the three altitudes.

Complete step by step solution:
Let us plot these points on the x-y plane as shown below.

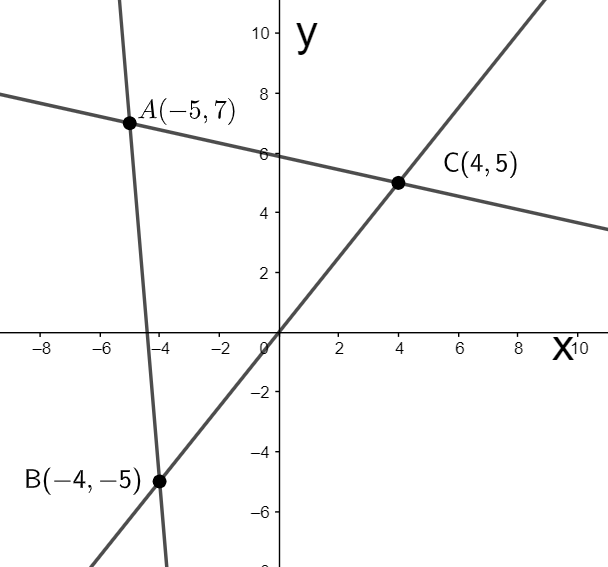
Let the altitudes of the given triangle be AP, BQ, and CR, from the vertices A, B, and C of the triangle ABC respectively, as shown in the below figure.
Let us now find out the slopes of the sides AB, BC and AC of the given triangle. We know that the slope of a line is given by
⇒m=y2−y1x2−x1\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}
Therefore, the slope of the side AB will be
⇒mAB=−5−7−4−(−5) ⇒mAB=−121 ⇒mAB=−12.........(i) \begin{aligned} & \Rightarrow {{m}_{AB}}=\dfrac{-5-7}{-4-\left( -5 \right)} \\\ & \Rightarrow {{m}_{AB}}=\dfrac{-12}{1} \\\ & \Rightarrow {{m}_{AB}}=-12.........\left( i \right) \\\ \end{aligned}
Similarly, the slope of the side BC will be

& \Rightarrow {{m}_{BC}}=\dfrac{5-\left( -5 \right)}{4-\left( -4 \right)} \\\ & \Rightarrow {{m}_{BC}}=\dfrac{10}{8} \\\ & \Rightarrow {{m}_{BC}}=\dfrac{5}{4}.........\left( ii \right) \\\ \end{aligned}$$ And the slope of the side AC will be $$\begin{aligned} & \Rightarrow {{m}_{AC}}=\dfrac{5-7}{4-\left( -5 \right)} \\\ & \Rightarrow {{m}_{AC}}=\dfrac{-2}{9} \\\ & \Rightarrow {{m}_{AC}}=-\dfrac{2}{9}.........\left( iii \right) \\\ \end{aligned}$$ We know that the altitude is a line passing through the vertex of a triangle and perpendicular to the side opposite to the vertex. Therefore, the altitude AP will be perpendicular to the side BC of the triangle ABC. Similarly the altitudes BQ and CR will be perpendicular to the sides AC and AB respectively. We know that the slopes of two perpendicular lines are related by $\Rightarrow {{m}_{1}}{{m}_{2}}=-1$ Therefore, the slope of the altitude AP will be given by $$\begin{aligned} & \Rightarrow {{m}_{AP}}{{m}_{BC}}=-1 \\\ & \Rightarrow {{m}_{AP}}=\dfrac{-1}{{{m}_{BC}}} \\\ \end{aligned}$$ Substituting (ii) we get $\Rightarrow {{m}_{AP}}=-\dfrac{4}{5}$ Similarly the slope of the altitude BQ is $$\Rightarrow {{m}_{BQ}}=\dfrac{-1}{{{m}_{AC}}}$$ Substituting the equation (ii) $$\Rightarrow {{m}_{BQ}}=\dfrac{9}{2}$$ Similarly, the slope of the altitude CR will be $$\Rightarrow {{m}_{CR}}=\dfrac{-1}{{{m}_{AB}}}$$ Substituting the equation (i) $$\Rightarrow {{m}_{BQ}}=12$$ Hence, we have finally obtained the slopes of the altitudes AP, BQ and CR to be $-\dfrac{4}{5}$, $\dfrac{9}{2}$ and $12$. **Note:** We can also determine the equations of all the three sides by using the two point form for the line. From there, we can determine the slope of the three sides and using the relation ${{m}_{1}}{{m}_{2}}=-1$ we can determine the slopes of all the three altitudes.