Solveeit Logo
Login

Question

Question: The vertex of the parabola \[x^{2}=8y-1\] (A). \[\left( \dfrac{-1}{8} ,0\right) \] (B). \[\left...

The vertex of the parabola x2=8y−1x^{2}=8y-1
(A). (−18,0)\left( \dfrac{-1}{8} ,0\right)
(B). (18,0)\left( \dfrac{1}{8} ,0\right)
(C). (0,18)\left( 0,\dfrac{1}{8} \right)
(D). (0,−18)\left( 0,\dfrac{-1}{8} \right)

Explanation

Solution

Hint: In this question it is given that we have to find the coordinate of the vertex of the parabola x2=8y−1x^{2}=8y-1. So to find the vertex of a parabola we need to know about the basic characteristics of a parabola, i.e, if any equation of a parabola is given like (x−h)2=4a(y−k)\left( x-h\right)^{2} =4a\left( y-k\right) then the coordinate of vertex is (h, k), so by using this concept we can easily find the vertex of the given parabola.

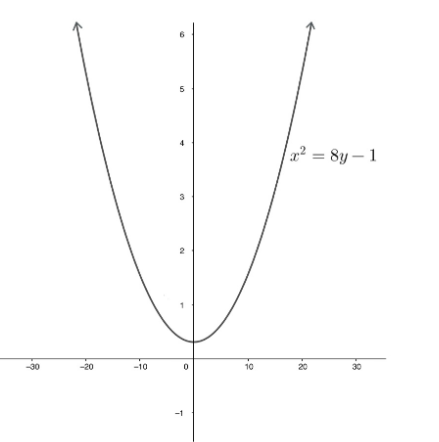
Complete step-by-step solution:
The given equation of parabola is x2=8y−1x^{2}=8y-1 .
So the above equation also can be rearrange as,
x2=8y−1x^{2}=8y-1
⇒x2=8(y−18)\Rightarrow x^{2}=8\left( y-\dfrac{1}{8} \right) [taking 8 common]
⇒(x−0)2=8(y−18)\Rightarrow \left( x-0\right)^{2} =8\left( y-\dfrac{1}{8} \right)
⇒(x−0)2=4×2(y−18)\Rightarrow \left( x-0\right)^{2} =4\times 2\left( y-\dfrac{1}{8} \right) .........(1)
Now comparing the above equation (1) with (x−h)2=4a(y−k)\left( x-h\right)^{2} =4a\left( y-k\right) , we can write,
h=0, k=18, a=2h=0,\ k=\dfrac{1}{8} ,\ a=2
And as we know that the vertex of any parabola (x−h)2=4a(y−k)\left( x-h\right)^{2} =4a\left( y-k\right) is (h,k) then we can say that the vertex of the given parabola is (0,18)\left( 0,\dfrac{1}{8} \right)
Hence the correct option is option C.

Note: While solving any parabola related problem you need to know that the point at which the axis intersects the parabola is called the vertex of the parabola. Also the given parabola is in the form of (x−h)2=±4a(y−k)\left( x-h\right)^{2} =\pm 4a\left( y-k\right) , and if any equation is in this form then its vertex is always parallel to y-axis, and depending upon the sign the the parabola opens, like if (x−h)2=4a(y−k)\left( x-h\right)^{2} =4a\left( y-k\right) then it opens to the upward direction and if (x−h)2=−4a(y−k)\left( x-h\right)^{2} =-4a\left( y-k\right) then the parabola opens down. But in this case the given parabola opens in the upward side i.e, in the positive direction of the y-axis.
And if the equation is in the form of (y−k)2=±4a(x−h)\left( y-k\right)^{2} =\pm 4a\left( x-h\right) the the vertex of the parabola is x axis and similarly the by the sign the parabola opens either right side(+ve x-axis) or left side(-ve x-axis).