Question

The vertex of the locus of a point that divides a chord of slope 2 of the parabola ${{y}^{2}}=4x$ internally in the ratio 1:2 is?
(a) $\left( \dfrac{1}{9},\dfrac{2}{9} \right)$
(b) $\left( \dfrac{8}{9},\dfrac{1}{9} \right)$
(c) $\left( \dfrac{2}{9},\dfrac{8}{9} \right)$
(d) $\left( \dfrac{1}{9},\dfrac{1}{9} \right)$

Answer 1

Assume two general point on the parabola in parametric form as $M\left( {{t}_{1}}^{2},2{{t}_{1}} \right)$ and $N\left( {{t}_{2}}^{2},2{{t}_{2}} \right)$. Find the slope of line MN by using the relation slope = $\dfrac{\Delta y}{\Delta x}$ and form a relation between ${{t}_{1}}$ and ${{t}_{2}}$. Now, consider point P(x, y) on the line MN such that MP:NP = 1:2 and use the section formula to given as $x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$ and $y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$ to form relations between $x,y,{{t}_{1}}$ and ${{t}_{2}}$. Here, consider $\left( {{x}_{1}},{{y}_{1}} \right)$ as the coordinates of M and $\left( {{x}_{2}},{{y}_{2}} \right)$ as the coordinates of N. Eliminate the variables ${{t}_{1}}$ and ${{t}_{2}}$, form an equation in x and y that will be the locus of the point P. Write the obtained locus in the form ${{\left( y-k \right)}^{2}}=4b\left( x-h \right)$ and get the vertex as (h, k).

Complete step by step answer:
Here we have been provided with the parabola ${{y}^{2}}=4x$ and its chord has slope 2 which is divided by a point in the ratio 1:2. We have to determine the vertex of the locus of that point. Let us draw a diagram of the given situation.

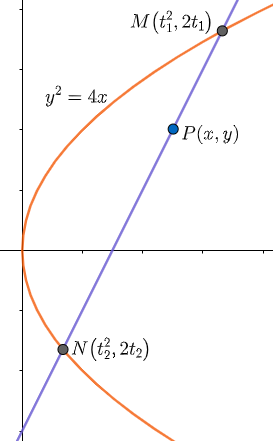
Now, in the above figure we have assumed the two points on the parabola as M and N. The point dividing this line segment MN is assumed as P(x, y). We know that any point on the parabola ${{y}^{2}}=4ax$ is assumed as $\left( a{{t}^{2}},2at \right)$ so on comparing ${{y}^{2}}=4x$ with ${{y}^{2}}=4ax$ we have a = 1. Therefore, the two points on the parabola can be assumed as $M\left( {{t}_{1}}^{2},2{{t}_{1}} \right)$ and $N\left( {{t}_{2}}^{2},2{{t}_{2}} \right)$.
We know that the slope of a line joining two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as $\dfrac{\Delta y}{\Delta x}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$, so considering point M as $\left( {{x}_{1}},{{y}_{1}} \right)$ and point N as $\left( {{x}_{2}},{{y}_{2}} \right)$ we have,
$\Rightarrow \dfrac{\Delta y}{\Delta x}=\dfrac{2{{t}_{2}}-2{{t}_{1}}}{{{t}_{2}}^{2}-{{t}_{1}}^{2}}$
Substituting the given value of slope we get,

& \Rightarrow 2=\dfrac{2{{t}_{2}}-2{{t}_{1}}}{{{t}_{2}}^{2}-{{t}_{1}}^{2}} \\\ & \Rightarrow 2=\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)} \\\ & \Rightarrow {{t}_{2}}+{{t}_{1}}=1............\left( i \right) \\\ \end{aligned}$$ Since, point P(x, y) divides the line MN is the ratio 1:2 so we have MP:NP = 1:2 = m:n ,so using the section formula given as $x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$ and $y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$ to determine the coordinates x and y we get, (i) For x – coordinate we have, $\begin{aligned} & \Rightarrow x=\dfrac{1\times {{t}_{2}}^{2}+2\times {{t}_{1}}^{2}}{1+2} \\\ & \Rightarrow x=\dfrac{{{t}_{2}}^{2}+2{{t}_{1}}^{2}}{3} \\\ & \Rightarrow 3x={{t}_{2}}^{2}+2{{t}_{1}}^{2}.........\left( ii \right) \\\ \end{aligned}$ (ii) For y – coordinate we have, $\begin{aligned} & \Rightarrow y=\dfrac{1\times 2{{t}_{2}}+2\times 2{{t}_{1}}}{1+2} \\\ & \Rightarrow y=\dfrac{2\left( {{t}_{2}}+2{{t}_{1}} \right)}{3} \\\ & \Rightarrow \dfrac{3y}{2}={{t}_{2}}+2{{t}_{1}}.........\left( iii \right) \\\ \end{aligned}$ Substituting the value of ${{t}_{1}}$ in terms of ${{t}_{2}}$ from equation (i) in equation (ii) we get, $\begin{aligned} & \Rightarrow 3x={{t}_{2}}^{2}+2{{\left( 1-{{t}_{2}} \right)}^{2}} \\\ & \Rightarrow 3x={{t}_{2}}^{2}+2\left( 1+{{t}_{2}}^{2}-2{{t}_{2}} \right) \\\ & \Rightarrow 3x=3{{t}_{2}}^{2}-4{{t}_{2}}+2..............\left( iv \right) \\\ \end{aligned}$ Substituting the value of ${{t}_{1}}$ in terms of ${{t}_{2}}$ from equation (i) in equation (ii) we get, $\begin{aligned} & \Rightarrow \dfrac{3y}{2}={{t}_{2}}+2\left( 1-{{t}_{2}} \right) \\\ & \Rightarrow \dfrac{3y}{2}=-{{t}_{2}}+2 \\\ & \Rightarrow {{t}_{2}}=\left( 2-\dfrac{3y}{2} \right)..........\left( v \right) \\\ \end{aligned}$ Now, substituting the value of ${{t}_{2}}$ from equation (v) in equation (iv) we get, $\begin{aligned} & \Rightarrow 3x=3{{\left( 2-\dfrac{3y}{2} \right)}^{2}}-4\left( 2-\dfrac{3y}{2} \right)+2 \\\ & \Rightarrow 3x=3\left( \dfrac{9{{y}^{2}}}{4}+4-6y \right)-4\left( 2-\dfrac{3y}{2} \right)+2 \\\ & \Rightarrow 3x=\dfrac{3}{4}\left( 9{{y}^{2}}+16-24y \right)-8+6y+2 \\\ \end{aligned}$ Multiplying both the sides with 4 and then dividing with 3 we get, $$\Rightarrow 4x=9{{y}^{2}}-16y+8$$ Using completing the square method in the R.H.S we get, $$\begin{aligned} & \Rightarrow 4x={{\left( 3y-\dfrac{8}{3} \right)}^{2}}+\dfrac{8}{9} \\\ & \Rightarrow 4x-\dfrac{8}{9}=9{{\left( y-\dfrac{8}{9} \right)}^{2}} \\\ & \Rightarrow \dfrac{4}{9}\left( x-\dfrac{2}{9} \right)={{\left( y-\dfrac{8}{9} \right)}^{2}} \\\ & \therefore {{\left( y-\dfrac{8}{9} \right)}^{2}}=\dfrac{4}{9}\left( x-\dfrac{2}{9} \right) \\\ \end{aligned}$$ Clearly the locus of point P is a parabolic equation of the form ${{\left( y-k \right)}^{2}}=4b\left( x-h \right)$ whose vertex is given as (h, k), so we have the vertex of parabola as $\left( \dfrac{2}{9},\dfrac{8}{9} \right)$. **So, the correct answer is “Option c”.** **Note:** Remember to always assume the unknown point on the parabola in parametric form otherwise if you assume it as any general variable represented by some alphabets then the calculation may become hard sometimes. Locus of a point is also known as the path traced by the point. Remember the general equation of all the curves like parabola, hyperbola, ellipse, circle etc.