Solveeit Logo
Login

Question

Question: The vertex of a parabola is (a, 0) and the directrix is x + y = 3a. The equation of the parabola is ...

The vertex of a parabola is (a, 0) and the directrix is x + y = 3a. The equation of the parabola is
A. x2−2xy+y2+6ax+10ay−7a2=0{x^2} - 2xy + {y^2} + 6ax + 10ay - 7{a^2} = 0
B. x2+2xy+y2+6ax+10ay+2a2=0{x^2} + 2xy + {y^2} + 6ax + 10ay + 2{a^2} = 0 = 0
C. x2+2xy+y2+6ax+10ay=2a2{x^2} + 2xy + {y^2} + 6ax + 10ay = 2{a^2}
D. None of these

Explanation

Solution

The axis of the parabola is perpendicular to the directrix and passes through the vertex. The equation of the directrix is given. Hence one can easily find the equation of the axis of the parabola.
Next, find the focus S (Note that vertex is the midpoint of foot of directrix and focus).
Now by definition, from any point P on the parabola, if we draw PM↔\overleftrightarrow {{\text{PM}}} perpendicular to the directrix,
then PS2=PM2{PS}^{2}={PM}^2

Complete step-by-step answer:
__
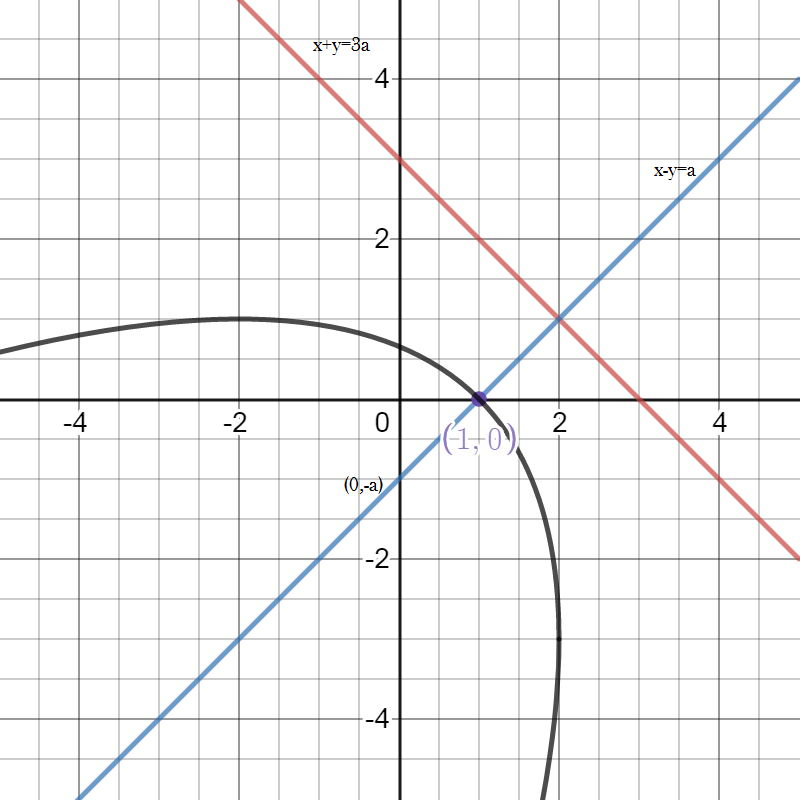
Given, the vertex is at (a, 0) and the directrix is x + y = 3a
The slope of the line perpendicular to the directrix x + y= 3a is 1
Since, the axis of the parabola is perpendicular to the directrix, the equation of the axis is x−y=cx - y = c , say. Since the axis passes through the vertex (a, 0), we substitute x=a, y=0 in the equation x−y=cx - y = c.
⇒a−0=c ⇒a=c  \Rightarrow a - 0 = c \\\ \Rightarrow a = c \\\
∴ The equation of the axis is x−y=ax - y = a
Now, solving the equations of the directrix and the axis ,we get the foot of the directrix (2a,a)
Again, we know vertex is the midpoint of the foot of the directrix and focus.
∴ focus is at S≡(0,−a)
Next, from any point P on the parabola, draw PM↔\overleftrightarrow {{\text{PM}}} perpendicular to the directrix.
From the definition of parabola, we know PS2=PM2{PS}^{2}={PM}^2

(x−0)2+(y+a)2=(x+y−3a2)2 On simplifying we get, ⇒2x2+2y2+4ay+2a2=x2+y2+9a2+2xy−6ax−6ay ⇒x2+y2−2xy+6ax+10ay−7a2=0  {(x - 0)^2} + {(y + a)^2} = {\left( {\dfrac{{x + y - 3a}}{{\sqrt 2 }}} \right)^2} \\\ {\text{On simplifying we get,}} \\\ \Rightarrow 2{x^2} + 2{y^2} + 4ay + 2{a^2} = {x^2} + {y^2} + 9{a^2} + 2xy - 6ax - 6ay \\\ \Rightarrow {x^2} + {y^2} - 2xy + 6ax + 10ay - 7{a^2} = 0 \\\

Hence, option (A) is correct.

Note: Note that, from any point P on the parabola, if we draw PM↔\overleftrightarrow {{\text{PM}}} perpendicular to the directrix.
then PS2=PM2{PS}^{2}={PM}^2 , where S is the focus of the parabola.