Question

The vertex A of a parabola is joined to any point P on the curve and PQ is drawn at right angles to AP to meet the axis in Q. Prove that the projection of PQ on the axis is always equal to the latus rectum.

Answer 1

In these type of questions, According to the parametric form, we will consider that the equation of parabola as ${y^2} = 4ax$, now again we will take any point P and its coordinates as $\left( {a{t^2},2at} \right)$, after that we will find the slope line AP, and with that slope we have to find the slope of the line PQ, and after that we have to write the equation of the line PQ passing through the point P, next we have to substitute $y = 0$ in the equation to find the point Q, next then we will find the length of the projection.

Complete step-by-step answer:
Given the vertex A of a parabola is joined to any point P on the curve and PQ is drawn at right angles to AP to meet the axis in Q ,
Here we have to prove that the projection of PQ on the axis is always equal to the latus rectum.
A latus rectum of a parabola is a double ordinate passing through the focus or a focal chord and perpendicular to the axis of parabola, now we will consider the equation of parabola ${y^2} = 4ax$,
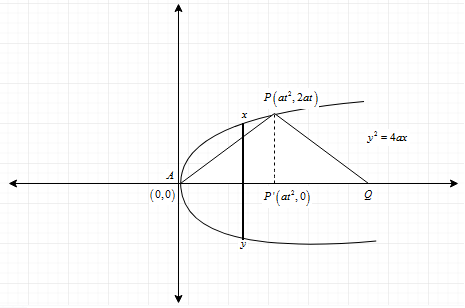
Now we will draw diagram regarding to the data given in the question,

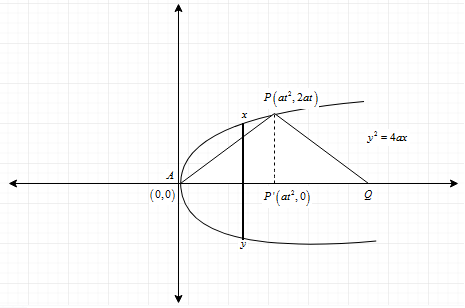
Now from the diagram drawn the parabola is given by ${y^2} = 4ax$ , now we will take any point P and its coordinates as $\left( {a{t^2},2at} \right)$, in the given question projection of line PQ on the axis will be P’Q , according to the given question we have to find the length of P’Q. From the figure P’P is the perpendicular to the x-axis, therefore the coordinates of P’ will be$P'\left( {a{t^2},0} \right)$, so to find the length of P’Q we have to find the coordinates of Q.
Now using slope formula we have to calculate the slope of the line AP, formula is given by,
$\Rightarrow$ Slope$= \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$,
Here ${x_1} = 0,{y_1} = 0,{x_2} = a{t^2},{y_2} = 2at$, now substituting the values we get,
$\Rightarrow$ Slope=$= \dfrac{{2at - 0}}{{a{t^2} - 0}}$,
Now simplifying we get,
$\Rightarrow$ Slope=$\dfrac{2}{t}$,
Now from the given data, PQ is perpendicular to AP, so according to the relation based on perpendicular lines we get,${m_1}{m_2} = - 1$, so here
${m_1} = \dfrac{2}{t}$, and ${m_2} =$ slope of PQ,
$\therefore \left( {\dfrac{2}{t}} \right){m_2} = - 1$,
By taking constant term to the other side we get,
$\Rightarrow {m_2} = - \dfrac{t}{2}$,
Now we got the slope of the line and we have to find the equation of the line PQ, from the formula of equation passing through a point $\left( {{x_1},{y_1}} \right)$ is given by,
$\Rightarrow$ $\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$,
Now using the formula and here ${y_1} = 2at,{x_1} = a{t^2}$ and $m = \dfrac{{ - t}}{2}$,
By substituting the values we get,
$\Rightarrow$ $y - 2at = \dfrac{{ - t}}{2}\left( {x - a{t^2}} \right)$,
Now we should find the coordinates of Q, as from the figure Q lies on x-axis its y-coordinate will be zero. So the equation becomes,
$\Rightarrow$ $0 - 2at = \dfrac{{ - t}}{2}\left( {x - a{t^2}} \right)$,
Simplifying we get,
$\Rightarrow - 2at = \dfrac{{ - t}}{2}\left( {x - a{t^2}} \right)$,
Now taking denominator to the L.H.S we get,
$\Rightarrow - 4at = - t\left( {x - a{t^2}} \right)$,
Now eliminating like terms and the negative sign we get,
$\Rightarrow 4a = x - a{t^2}$,
Now taking all constant terms to one side we get,
$\Rightarrow x = 4a + a{t^2}$,
Now the coordinate of Q are $\left( {4a + a{t^2},0} \right)$,
Now we will find the latus rectum of the parabola, from the figure is clear that it is length xy, now the coordinates of x are to be determined and in this case x-coordinate of x will be a, so we have,
$\Rightarrow$ ${y^2} = 4ax$,
Here$x = a$, so the equation becomes,
$\Rightarrow$ ${y^2} = 4a\left( a \right)$,
$\Rightarrow {y^2} = 4{a^2}$,
$\Rightarrow y = 2a$and $\Rightarrow y = - 2a$,
So, we got the coordinates of x and y they are $x\left( {a,2a} \right)$and$y\left( {a, - 2a} \right)$, so now the length of latus rectum =$2a - \left( { - 2a} \right)$=$4a$,
Now we have to find the length of P’Q, which is equal to
$\Rightarrow$ $P'Q = AQ - AP'$,
Now substituting the values we get,
$\Rightarrow$ $P'Q = \left( {a{t^2} + 4a} \right) - a{t^2}$,
Releasing the brackets and subtracting we get,
$\Rightarrow$ $P'Q = 4a$,
Thus, from the above P’Q= length of the latus rectum.

It is proven that the projection of PQ on the axis is always equal to the latus rectum. Hence proved.

Note:
Here we had consider that the equation of parabola is ${y^2} = 4ax$, and proved the above question but here we can also assume that the equation of parabola can be ${x^2} = 4ay$, in either ways the length of the projection will be equal to the length of the latus rectum.