Question

The vertex A of a parabola is joined to any point P on the curve and PQ is drawn at right angles to AP to meet the axis in Q. Prove that the projection of PQ on the axis is always equal to the latus rectum.

Answer 1

Hint: To solve this question, we will assume the equation of parabola as ${{y}^{2}}=4ax$ . Then we will take point P and we will take its point as $P\left( a{{t}^{2}},2at \right)$ according to the parametric form. Then we will find the slope of line AP and with the help of that slope, we will find the slope of line PQ. After finding slope, we will write the equation of the line PQ passing through point P. Then we will put $y=0$ in that equation to obtain the point Q. Here we will find the length of projection.

Complete step-by-step answer:
Before solving the question, we must know what a latus rectum. A latus rectum of a parabola is a double ordinate passing through the focus or a focal chord and perpendicular to the axis of parabola. Now, we will assume a general parabola ${{y}^{2}}=4ax$.

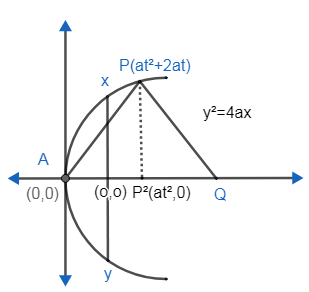
Here, we have drawn the parabola ${{y}^{2}}=4ax$. We have considered the general point P as $P\left( a{{t}^{2}},2at \right)$ according to the parametric form of parabola. In this case, the projection of line PQ on the axis is P’Q. We have to find the length of the line P’Q. We know that PP’ is perpendicular to the x-axis. Thus the coordinates of $P'$ are $=P'\left( a{{t}^{2}},0 \right)$ . We will have to find the coordinates of Q to find the length P’Q.
Now, we will calculate the slope of line AP. It is given by the formula:
Slope $=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
After applying this formula, we get:
Slope of AP $=\dfrac{2at-0}{a{{t}^{2}}-0}=\dfrac{2at}{a{{t}^{2}}}=\dfrac{2}{t}$
Let slope of AP $={{m}_{1}}=\dfrac{2}{t}$ ………………… (1)
Now, we are given that the line PQ is perpendicular to AP. So, according to the relation between the slopes of parallel lines, we have:
${{m}_{1}}{{m}_{2}}=-1$
Here, we have $={{m}_{1}}=\dfrac{2}{t}$ and ${{m}_{2}}$is the slope of PQ.
Thus $\left( \dfrac{2}{t} \right){{m}_{2}}=-1$ (from (1) ${{m}_{1}}=\dfrac{2}{t}$ )
$\Rightarrow {{m}_{2}}=\dfrac{-t}{2}$ ………………………… (2)
Now, we know the slope of the line PQ, so we can find the equation of line PQ. The equation of a line passing through a point $\left( {{x}_{1}},{{y}_{1}} \right)$ and having slope is given by:
$\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$
Thus, applying above formula, we have:
$\left( y-{{y}_{1}} \right)=\left( \dfrac{-t}{2} \right)\left( x-{{x}_{1}} \right)$
In our case, the line passes through the point P so ${{y}_{1}}=2at$ and ${{x}_{1}}=a{{t}^{2}}$ . Thus, we get:
$\left( y-2at \right)=\left( \dfrac{-t}{2} \right)\left( x-a{{t}^{2}} \right)$ ………………………….. (3)
Now, we have to find the coordinates of Q. We know that Q is in the x axis. So, its y coordinates are zero. Let its x coordinates be ${{x}_{Q}}$ . thus, from (3), we have:
$\begin{aligned} & \left( 0-2at \right)=\left( \dfrac{-t}{2} \right)\left( {{x}_{Q}}-a{{t}^{2}} \right) \\\ & \Rightarrow -2at=\left( \dfrac{-t}{2} \right)\left( {{x}_{Q}}-a{{t}^{2}} \right) \\\ & \Rightarrow \dfrac{-4at}{-t}={{x}_{Q}}-a{{t}^{2}} \\\ & \Rightarrow 4a={{x}_{Q}}-a{{t}^{2}} \\\ \end{aligned}$
$\Rightarrow {{x}_{Q}}=a{{t}^{2}}+4a$…………………………….. (4)
From (4), we have got: $Q\left( a{{t}^{2}}+4a,0 \right)$
Now, we will find the latus rectum of this parabola. In our case, it is the length XY in the figure drawn. We will now find the coordinates of X. in this x coordinates of X is a. So, we have:
$\begin{aligned} & {{y}^{2}}=4ax \\\ & {{y}^{2}}=4a\left( a \right) \\\ & \Rightarrow {{y}^{2}}=4{{a}^{2}} \\\ & \Rightarrow y=2a\text{ and }y=-2a \\\ \end{aligned}$
Thus, we have: $X\left( a,2a \right)\text{ and }Y\left( a,-2a \right)$ . Thus the length of latus rectum $=2a-\left( -2a \right)=4a$ .
Now, we will find the length of P’Q. It is equal to:
$\begin{aligned} & P'Q=AQ-AP' \\\ & P'Q=\left( a{{t}^{2}}+4a \right)-\left( a{{t}^{2}} \right) \\\ & P'Q=4a \\\ \end{aligned}$
Thus P’Q = latus rectum length of parabola.

Note: We have assumed the equation of parabola as ${{y}^{2}}=4ax$ . Instead of this, we could have also chosen any other parabola like ${{x}^{2}}=4ay$. The thing to note is that, in any parabola, the length of the projection will be equal to the length of the latus rectum of that parabola.