Question
Question: The venture tube as shown in the figure is used as a fluid meter. Suppose the device is used at a se...
The venture tube as shown in the figure is used as a fluid meter. Suppose the device is used at a service station to measure the flow rate of gasoline ( ρ=7.0×102kgm−3 ) through a hose having outlets radius of 1.20cm . If the difference in pressure is measured as P1−P2=1.2kPa and the radius of inlet is 2.40cm.Find the speed of the gasoline as it leaves the hose.
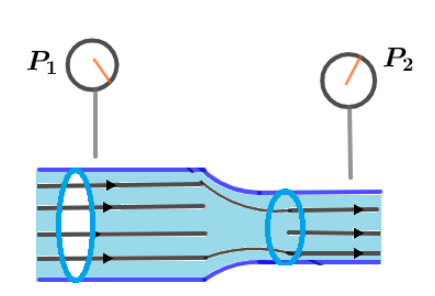
Solution
In order to solve the given question, we will use the concept of venture effect of fluids which states that, there always gets a reduction in fluid pressure when fluid passes through a choke or constricted section of a pipe and the relation between pressures is given as P1−P2=2ρ(v22−v12).
Formula used:
Rate of flow of fluid through a circular section at both ends of a venturi meter is constant and written as,
πr12v1=πr22v2
where, r1,r2 are the radii of inlet and outlet circular ends of the pipe.
Complete step by step answer:
Let us first find the velocity relation from given parameters using the relation of rate of flow, πr12v1=πr22v2 .
Given that, r1=2.40cm and r2=1.20cm put these values in equation πr12v1=πr22v2 we get,
(2.4)2v1=(1.2)2v2
⇒v2=4v1→(i)
Now, using the venturi effect formula, P1−P2=2ρ(v22−v12) we have given that,
P1−P2=1.2kPa
⇒ρ=7.0×102kgm−3
And put value of v2=4v1 we get,
P1−P2=2ρ(v22−v12)
⇒1.2×103=27.0×102(16v12−v12)
⇒724=15v12
⇒0.0519=v12
⇒v1=0.228msec−1
So from the relation v2=4v1 the outlet velocity of fluid is
v2=4×0.228
∴v2=1.91msec−1
Hence, the velocity at which gasoline leaving hose is v2=1.91msec−1.
Note: It should be remembered that, Venturi meter is a device which is used to determine the rate of flow of a fluid through a pipe and rate of flow is taken as product of area of cross section of pipe and the velocity at which it enters, the basic unit of conversion must be remembered as 1kPa=103Pa .
