Question

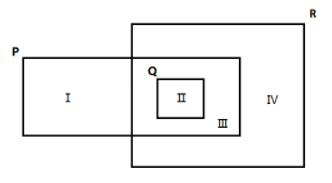
The Venn diagram shows sets $P$, $Q$ and $R$with regions labelled, Ⅰ, Ⅱ, Ⅲ and Ⅳ. State the regions which represents set $\left[ {P \cap {{\left( {Q \cup R} \right)}^\prime }} \right]$

1. Ⅰ
2. Ⅱ
3. Ⅲ
4. Ⅳ

Answer 1

Firstly, find the region of the inside bracket,$\left( {Q \cup R} \right)$ which includes the region including both $Q$ and $R$. Next, take the compliment of the region $\left( {Q \cup R} \right)$ by excluding the region $\left( {Q \cup R} \right)$ from the universal set or all regions. Lastly, solve $\left[ {P \cap {{\left( {Q \cup R} \right)}^\prime }} \right]$ by taking the common region of set $P$and compliment of $\left( {Q \cup R} \right)$ to find the required region.

Complete step by step solution: We can determine the region $\left( {Q \cup R} \right)$ by finding the union of $Q$ with$R$, that is the region which includes both the sets $Q$ and $R$.
As, it is seen from the diagram, region Ⅱ, Ⅲ and Ⅳ includes the set $Q$ and $R$.
Next, take the compliment of the region $\left( {Q \cup R} \right)$, that is, take the region excluding Ⅱ , Ⅲ and Ⅳ from the given diagram.
The region left after excluding the region Ⅱ, Ⅲ and Ⅳ is region Ⅰ.
We can see from the diagram, set $P$includes region Ⅰ, Ⅱ and Ⅲ.
Now, to solve the expression $\left[ {P \cap {{\left( {Q \cup R} \right)}^\prime }} \right]$ take the intersection of set $P$ and ${\left( {Q \cup R} \right)^\prime }$, that is take the region with is common in set $P$ and ${\left( {Q \cup R} \right)^\prime }$.
The region Ⅰ is the common region of set $P$ and ${\left( {Q \cup R} \right)^\prime }$.
Hence, $\left[ {P \cap {{\left( {Q \cup R} \right)}^\prime }} \right]$ represents region Ⅰ.

Note: Students often get confused with the symbols of union and intersection. $\cup$ represents union between two sets and $\cap$ represents intersection of the two sets. Identify the regions corresponding to the sets correctly. A single set may include more than one regions. Also, look at the given Venn diagram carefully before selecting the region.