Question

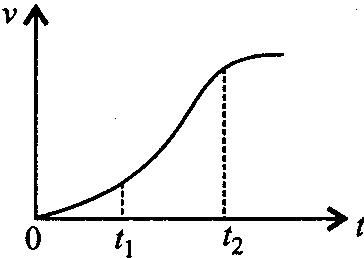
The velocity-time graph of a particle in one-dimensional motion is shown in the figure. Which of the following formulae is correct for describing the motion of the particle over the time interval $\mathrm { t } _ { 1 }$ to $_ { 2 }$ ?

• A. $x \left( t _ { 2 } \right) = x \left( t _ { 1 } \right) + v \left( t _ { 1 } \right) \left( t _ { 2 } - t _ { 1 } \right) + \left( \frac { 1 } { 2 } \right) a \left( t _ { 2 } - t _ { 1 } \right) ^ { 2 }$
• B. $\mathrm { v } \left( \mathrm { t } _ { 2 } \right) = \mathrm { v } \left( \mathrm { t } _ { 1 } \right) + \mathrm { a } \left( \mathrm { t } _ { 2 } - \mathrm { t } _ { 1 } \right)$
• C. $\mathrm { v } _ { \text {average } } = \frac { \left( \mathrm { x } \left( \mathrm { t } _ { 2 } \right) + \mathrm { x } \left( \mathrm { t } _ { 1 } \right) \right) } { \left( \mathrm { t } _ { 2 } - \mathrm { t } _ { 1 } \right) }$
• D. $\mathrm { a } _ { \text {average } } = \frac { \left( \mathrm { v } \left( \mathrm { t } _ { 2 } \right) - \mathrm { v } \left( \mathrm { t } _ { 1 } \right) \right) } { \left( \mathrm { t } _ { 2 } - \mathrm { t } _ { 1 } \right) }$

Answer 1

Answer: (D)

$\mathrm { a } _ { \text {average } } = \frac { \left( \mathrm { v } \left( \mathrm { t } _ { 2 } \right) - \mathrm { v } \left( \mathrm { t } _ { 1 } \right) \right) } { \left( \mathrm { t } _ { 2 } - \mathrm { t } _ { 1 } \right) }$

Answer 2

In the given interval the slope of v-t graph (i.e. accelerations) neither constant nor uniform . Therefore relations (1), (2) and (3) are incorrect but (4) is correct.