Question

The velocity-time graph of a car and a scooter are shown in the figure. (i) The difference between the distance travelled by the car and the scooter in 15 s and (ii) The time at which the car will catch up with the scooter are, respectively:

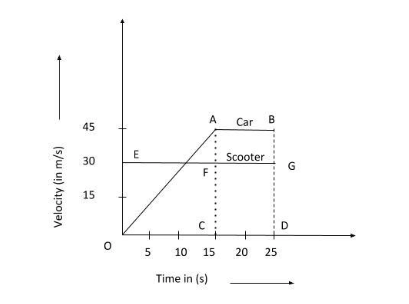
A) 112.5 m & 22.5 s
B) 337.5 m & 25 s
C) 112.5 m & 15 s
D) 225.5 m & 10 s

Answer 1

In the question we have been provided with the velocity - time graph of a scooter and a car and we are asked to find the difference between the distance travelled by each of these vehicles. Such types of questions can be verbally solved if one can properly read the graph. Here, the area under the graph of each vehicle gives you the distance travelled by that respective vehicle.

Complete step by step answer:

1. Difference between the distance travel by car and the scooter in 15 s :
   As discussed above the area under the velocity - time graph gives the distance travelled by the respective vehicle.
   Hence, distance travelled by the scooter in 15 s is given by the area of quadrilateral OEFC.
   ${s_{scooter}} = 15 \times 30 = 450m$
   Also, the distance travelled by the car in 15 s is given by the area of triangle ACO.
   ${s_{car}} = \dfrac{1}{2} \times 15 \times 45 = 337.5m$
   Now, the difference between the distance travelled by car and scooter in the time of 15 s is given by,
   $\Delta s = {s_{scooter}} - {s_{car}} = 450 - 337.5$
   $\Delta s = 112.5m$……….(1)

2. The time at which the car will catch up with the scooter :
   Let us consider that after some time (t) the car catches up with the scooter. Hence, we can say that, after time t the distance travelled by both car and the scooter will be equal. Mathematically, this can be written as,
   ${s_{scooter}} = {s_{car}}$
   $30t = \dfrac{1}{2} \times 15 \times 45 + 45 \times (t - 15)$
   $30t = 337.5 + 45t - 675$
   $t = 22.5s$……….(2)

Hence, from (1) & (2), we can say that option A is the correct answer option.

Note: Some of the key points to be remembered are given below.
-Velocity and displacement are vector quantities while speed and distance are scalar quantities.
-The area under the velocity - time graph will give you the distance travelled in particular time.
-The slope of the velocity - time $\left( {\dfrac{{dv}}{{dt}}} \right)$ graph gives us the acceleration.