Question
Question: The velocity time graph of a body is given in figure. The maximum acceleration in \(m/{{s}^{2}}\) is...
The velocity time graph of a body is given in figure. The maximum acceleration in m/s2 is
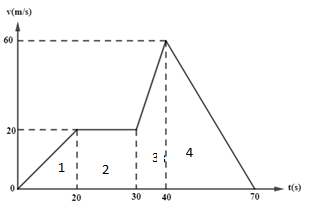
(a) 4
(b) 3
(c) 2
(d) 1
Solution
Hint: We know that acceleration of a body means the change in velocity of the body with respect to change in time. It can also be said that the slope of the v-t graph is given by acceleration and it can be seen mathematically as, a=ΔtΔv. Using this formula, we will find the maximum acceleration of the body.
Formula used: a=ΔtΔv
Complete step-by-step answer:
In question we are asked to find the maximum acceleration of the body from the given graph, but before that we will understand what is acceleration.
So, acceleration of a body means the change in velocity of the body with respect to change in time. It can also be said that slope of v-t graph is given by acceleration and it can be seen mathematically as, a=ΔtΔv …………………….(i)
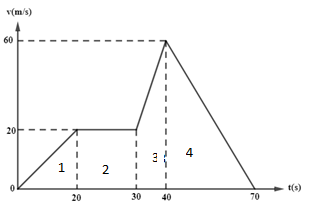
Now, to find the maximum acceleration we will find the graph in 4 parts.
In part 1, velocity of the body increases from 0 to 20 m/s with respect to time which changes from 0 to 20 seconds. So, from this it can be said that for part 1,
v1=0m/s and v2=20m/s, t1=0s and t2=20s
Now, substituting these values in expression (i) we will get,
a=t2−t1v2−v1=20−020−0
⇒a=2020=1m/s2
Now, for part 2, velocity remains constant and we know that when the value of y remains constant, the slope is zero so the acceleration of the body is also zero.
Now, for part 3, velocity of the body increases from 20 to 60 m/s with respect to time which changes from 30 to 40 seconds. So, from this it can be said that for part 3,
v1=20m/s and v2=60m/s, t1=30s and t2=40s
Now, substituting these values in expression (i) we will get,
a=t2−t1v2−v1=40−3060−20
⇒a=1040=4m/s2
Now, in part 4, after the velocity of the body reaches maximum its velocity reduces and becomes zero, so it is known as deceleration. So, from this it can be said that for part 4,
v1=60m/s and v2=0m/s, t1=60sand t2=70s
Now, substituting these values in expression (i) we will get,
a=t2−t1v2−v1=70−600−60
⇒a=10−60=−6m/s2
Thus, from this we can say that the maximum acceleration of the body is 4m/s2.
Hence, option (a) is the correct answer.
Note: Now, students might forget to consider the decrease in velocity from 60 to 0 as deceleration and they might consider as acceleration, by doing this the acceleration becomes a=1060=6m/s2. But it is wrong so students must be careful in problems of graphs and work accordingly.
