Question

The velocity of the air in a stream line flow is $200m{{s}^{-1}}$. The difference in the pressure between the air just over the wing ${{P}_{1}}$​ and that under the wing ${{P}_{2}}$ will be given as:

$\begin{aligned} & A.2.8\times {{10}^{3}}Pa \\\ & B.0.723\times {{10}^{2}}Pa \\\ & C.1.46\times {{10}^{4}}Pa \\\ \end{aligned}$

Answer 1

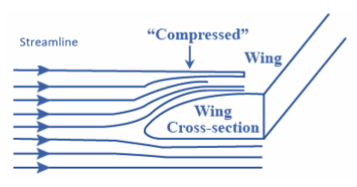
Compression of the streamlines is meant by the stream tube above the wing having a smaller cross-sectional area than that in front of the plane. Use the continuity equation to find the velocity above the wings. And also use Bernoulli's equation to find the pressure between the air just over the wing and under the wing.

Complete answer:
Compression of the streamlines means that the stream tube above the wing has a smaller cross-sectional area than that in front of the plane and from the continuity equation, the velocity ${v}'$ of the air must therefore be greater above the wing.
The area above the wing is found by the equation,
${A}'=\dfrac{8}{10}A$
That is, the ratio of the area will be given as,
$\dfrac{A}{{{A}'}}=\dfrac{10}{8}$
Using the continuity equation,
$Av={A}'{v}'$
Where $v$ be the velocity of air given,
$v=200m{{s}^{-1}}$
The velocity above the wing will be,
${v}'=\dfrac{A}{{{A}'}}v=\dfrac{10}{8}\times 200=250m{{s}^{-1}}$
The greater velocity ${v}'$ indicates the lower pressure than the normal pressure of the air in front of the plane. It is mentioned that the flow-lines under the wing are not compressed at all. The pressure under the wing will be the normal pressure of the air in front of the wing.
According to Bernoulli's equation, with both points 1 (for ${{P}_{1}}$) and 2 (for ${{P}_{2}}$) at effectively the same elevation.
${{P}_{a}}+\dfrac{1}{2}{{\rho }_{a}}{{v}_{1}}^{2}={{P}_{b}}+\dfrac{1}{2}{{\rho }_{b}}{{v}_{2}}^{2}$
As we already mentioned that the velocity of the air is,
${{v}_{2}}=v=200m{{s}^{-1}}$
Rearranging the equation will give,
${{P}_{2}}-{{P}_{1}}=\dfrac{1}{2}{{\rho }_{a}}\left( {{v}_{1}}^{2}-{{v}_{2}}^{2} \right)$
Let us substitute the values in it,
$\begin{aligned} & {{P}_{2}}-{{P}_{1}}=\dfrac{1}{2}\times 1.3\times \left( {{250}^{2}}-{{200}^{2}} \right) \\\ & {{P}_{2}}-{{P}_{1}}=1.46\times {{10}^{4}}Pa \\\ \end{aligned}$
Therefore the correct answer has been obtained.

It is given as option C.

Note:
Bernoulli's principle says that an increase in the speed of a fluid happens simultaneously with a decrease in static pressure or a decrease in the potential energy of the fluid. A continuity equation is a simple and powerful equation which describes the transport of quantities with the help of the area and velocity.