Question

The velocity of image of P1 seen by observer P2.

& A)-(8cm{{s}^{-1}})\widehat{i} \\\ & B)(8cm{{s}^{-1}})\widehat{i} \\\ & C)0 \\\ & D)(10cm{{s}^{-1}})\widehat{i} \\\ \end{aligned}$$

Answer 1

We will calculate the relative speed of P1 with respect to mirror because that speed will become the speed of image I from the object P1.Then we will calculate the relative speed of image formed by P1with respect to mirror. Finally the relative speed between I and P2 gives the result of velocity of image P1 seen by observer P2.

Complete step-by-step answer:
When an object, image and mirror all are moving then the concept of relative speed is applied to calculate the relative speed of any object , image or mirror. Here in this question the mirror is moving along with objects that are also moving. So, According to the figure, the mirror is moving with speed of $2m{{s}^{-1}}$ along the negative direction of the x axis.
Let us assume the velocity of the mirror is${{V}_{m}}=-2\widehat{i}$. Objects P1 and P2 are also moving in the negative direction of the x axis. So speed of these two objects can be represented as - Velocity of P1 is represented by${{V}_{{{P}_{1}}}}=-4\widehat{i}$. Velocity of P2 is represented by${{V}_{{{p}_{2}}}}=-8\widehat{i}$.

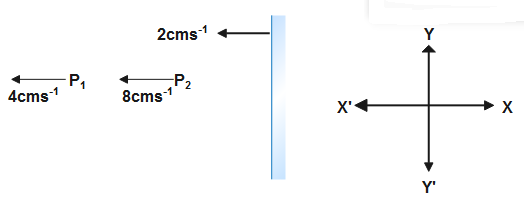
We will first calculate the relative velocity of P1 with respect to mirror M as both are moving, so we do it in a mathematical way. Let us assume this relative velocity can be represented as${{V}_{{{P}_{1}}M}}$. Now apply mathematical relation for relative speed, we get
$\overrightarrow{{{V}_{{{P}_{1}}M}}}=\overrightarrow{{{V}_{{{P}_{1}}}}}-\overrightarrow{{{V}_{M}}}$
$\Rightarrow \overrightarrow{{{V}_{{{P}_{1}}M}}}=(-4+2)\widehat{i}$
$\therefore \overrightarrow{{{V}_{{{P}_{1}}M}}}=-2\widehat{i}$
Let us assume the image of object P1 is represented by I. Now we will calculate the Relative velocity of Image I with respect to mirror M.
Let us assume the relative velocity of image I with respect to Mirror M is represented by $\overrightarrow{{{V}_{IM}}}$.
So velocity of image P1 is$\overrightarrow{{{V}_{I}}}=-2\widehat{i}$
Now apply mathematical relation for relative velocity, $\overrightarrow{{{V}_{IM}}}=\overrightarrow{{{V}_{I}}}-\overrightarrow{{{V}_{M}}}$

& \Rightarrow \overrightarrow{{{V}_{IM}}}=(-2+2)\widehat{i} \\\ & \therefore \overrightarrow{{{V}_{IM}}}=0 \\\ \end{aligned}$$ Now we will finally calculate the relative speed of Image formed by P1 with respect to P2. Let us assume this velocity as $$\overrightarrow{{{V}_{I{{P}_{2}}}}}=\overrightarrow{{{V}_{I}}}-\overrightarrow{{{V}_{{{P}_{2}}}}}$$ $$\Rightarrow \overrightarrow{{{V}_{I{{P}_{2}}}}}=(0+8)\widehat{i}$$ $$\therefore \overrightarrow{{{V}_{I{{P}_{2}}}}}=(8\widehat{i})cm{{s}^{-1}}$$ So the relative speed of P1 seen by observer P2 is acting along the positive direction of X axis whose magnitude is $$8cm{{s}^{-1}}$$. **So, the correct answer is “Option B”.** **Note:** When the object moves with speed u towards (or away) from the plane mirror then image also moves toward (or away) with speed u. But relative speed of image with respect to an object is 2u. When the mirror moves towards the stationary object with speed u, the image will move with speed 2u.