Question

The velocity of a projectile at any instant is $\text{u}$ making an angle $\text{ }\\!\\!\alpha\\!\\!\text{ }$ with the horizon. The time after which it will be moving at right angles to this direction is:
A) $\dfrac{u\cos ec\left( \alpha \right)}{g}$
B) $\dfrac{u\cos \left( \alpha \right)}{g}$
C) $\dfrac{u\sin \left( \alpha \right)}{g}$
D) $\dfrac{u\tan \left( \alpha \right)}{g}$

Answer 1

Hint: A projectile will have velocity components along the horizontal as well as the vertical direction. The projectile will be at right angles to the direction when the slope of the initial curve multiplied with the slope of the curve at time t gives -1.

Complete step by step answer:

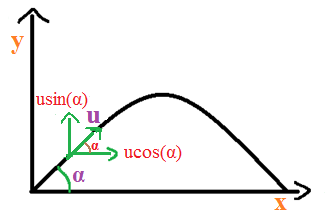
In the question, the projectile makes an angle $\text{ }\\!\\!\alpha\\!\\!\text{ }$ with the horizontal. So the initial components of velocity of the projectile at time t=0 along the x and y axes can be written as,
${{u}_{x}}=u\cos \left( \alpha \right)$ …. Equation (1)
${{u}_{y}}=u\sin \left( \alpha \right)$ ….. equation (2)
So the slope of the initial curve can be written as,
${{m}_{1}}=\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}$
$\dfrac{dy}{dt}\text{ and }\dfrac{dx}{dt}$ are the velocities along the y-axis $\left( {{u}_{y}} \right)$ and x-axis $\left( {{u}_{x}} \right)$ respectively at time t=0.
So, From equations (1) and (2), we can write,
${{m}_{1}}=\dfrac{u\sin \alpha }{u\cos \alpha }$
$\therefore {{m}_{1}}=\tan \alpha$ … Equation (3)
We know that the velocity along the horizontal direction remains constant, while the velocity along with the vertical direction changes due to acceleration due to gravity acting on it.
So the displacement components of the projectile at a time t, where the slope of the curve will be perpendicular to the initial curve is given by,
$x=ut\cos \alpha$ ……. Equation (4)
$y=ut\sin \alpha -\dfrac{1}{2}g{{t}^{2}}$ …. Equation (5)
Equation (4) came from the formula $x={{u}_{x}}t$ (since there is no acceleration along the x-axis). For Equation (5) we used the formula $y={{u}_{y}}t-\dfrac{1}{2}g{{t}^{2}}$ (the velocity since the acceleration due to gravity is acting on the body).
We can differentiate the Equations (4) and (5) w.r.t time to get the velocities along the x-axis and y-axis at the time ‘t’. So, we can write,
${{u}_{x}}=u\cos \alpha$… Equation (6)
${{u}_{y}}=u\sin \alpha -gt$… Equation (7)
So the slope of the current curve can be written as,
${{m}_{2}}=\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}$
$\dfrac{dy}{dt}\text{ and }\dfrac{dx}{dt}$ are the velocities along the y-axis $\left( {{u}_{y}} \right)$ and x-axis $\left( {{u}_{x}} \right)$ respectively at time t=’t’.
So, From Equation (6) and (7), we can write,
${{m}_{2}}=\dfrac{u\sin \alpha -gt}{u\cos \alpha }$… Equation (8)
So the product of ${{m}_{1}}$ and ${{m}_{2}}$ should be -1 for the projectile to move at right angles to each other.
${{m}_{1}}{{m}_{2}}=-1$
From equations (3) and (8), we get,
$\tan \alpha \left( \dfrac{u\sin \alpha -gt}{u\cos \alpha } \right)=-1$
$\Rightarrow \sin \alpha (u\sin \alpha -gt)=-u{{\cos }^{2}}\alpha$
$\Rightarrow u({{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha )=gt\sin \alpha$
$\therefore t=\dfrac{u\cos ec\alpha }{g}$
So the answer to the question is option (A)- $\dfrac{u\cos ec\alpha }{g}$

Note:
A projectile usually follows a parabolic path, except when the projectile is thrown upwards; in this case, it follows a straight-line path.
Acceleration along the x-axis is zero, so the projectile moves with constant velocity along the x-axis due to its inertia.