Solveeit Logo
Login

Question

Question: The velocities of light in two different media are \(2 \times {10^8}m{s^{ - 1}}\) and \(3.5 \times {...

The velocities of light in two different media are 2×108ms−12 \times {10^8}m{s^{ - 1}} and 3.5×108ms−13.5 \times {10^8}m{s^{ - 1}} respectively. The critical angle for these media is:
A. sin⁡−1(15){\sin ^{ - 1}}\left( {\dfrac{1}{5}} \right)
B. sin⁡−1(47){\sin ^{ - 1}}\left( {\dfrac{4}{7}} \right)
C. sin⁡−1(23){\sin ^{ - 1}}\left( {\dfrac{2}{3}} \right)
D. sin⁡−1(67){\sin ^{ - 1}}\left( {\dfrac{6}{7}} \right)

Explanation

Solution

Critical angle is the minimum angle of incidence required for the light for total internal reflection to occur. The speed of light is lesser in denser medium and more in rarer medium.

Complete step by step answer:
Refraction is defined as the process in which light travels from one medium to another.During refraction, a change in velocity and wavelength of light occurs, whereas frequency remains constant. Light travels faster in rarer medium and slower in denser medium.

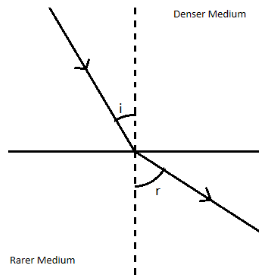
In the above figure, the light ray approaching the junction of two media is known as incident ray. And the light ray leaving the junction is known as refracted ray. The angle which incident ray forms with the normal is known as the incident angle(i)\left( i \right) and the angle which the refracted ray forms with the normal is known as the refracted angle(r)\left( r \right).

When the light travels from denser medium to rarer medium, its velocity increases and angle of incidence is greater than angle of refraction. As we start increasing the angle of incidence, the angle of refraction also increases. At a specific angle of incidence, the angle of refraction becomes 900{90^0}. That angle of incidence is known as critical angle(iC)\left( {{i_C}} \right). If we increase the angle of incidence more than the critical angle, then refraction stops occurring and reflection starts occurring. This reflection is known as Total Internal Reflection.

The value of critical angle can be given by Snell’s law, that is
iC=sin⁡−1(μRμD){i_C} = {\sin ^{ - 1}}\left( {\dfrac{{{\mu _R}}}{{{\mu _D}}}} \right)
Where, μR={\mu _R} = Refractive index of rarer medium and μD={\mu _D} = Refractive index of denser medium.
Now we know that,
μ∝1v\mu \propto \dfrac{1}{v}
Where, v=v = Velocity of light in the medium.
So,
μRμD=vDvR\dfrac{{{\mu _R}}}{{{\mu _D}}} = \dfrac{{{v_D}}}{{{v_R}}}
Where, vD={v_D} = Velocity of light in denser medium=2×108ms−1 = 2 \times {10^8}m{s^{ - 1}} and vR={v_R} = Velocity of light in rarer medium=3.5×108ms−1 = 3.5 \times {10^8}m{s^{ - 1}}. So the equation of Snell’s Law becomes,
iC=sin⁡−1(vDvR){i_C} = {\sin ^{ - 1}}\left( {\dfrac{{{v_D}}}{{{v_R}}}} \right)
⇒iC=sin⁡−1(2×1083.5×108)\Rightarrow {i_C} = {\sin ^{ - 1}}\left( {\dfrac{{2 \times {{10}^8}}}{{3.5 \times {{10}^8}}}} \right)
∴iC=sin⁡−1(47)\therefore {i_C} = {\sin ^{ - 1}}\left( {\dfrac{4}{7}} \right)

Hence, the correct answer is option B.

Note: Total Internal reflection is the basis of modern technology. Since most of the modern technology is based on the transaction and transfer of data and how fast one can achieve it. Now total internal reflection uses light, and no other entity discovered has a speed greater than that of light, thus total internal reflection is the fastest possible way for the transfer of data.