Question

The vector with initial point P (2, -3, 5) and terminal point Q (3, -4, 7) is
(a) $\hat{i}-\hat{j}+2\hat{k}$
(b) $5\hat{i}-7\hat{j}+12\hat{k}$
(c) $\hat{i}+\hat{j}-2\hat{k}$
(d) None of these

Answer 1

We must first find the position vectors $\overrightarrow{OP}\text{ and }\overrightarrow{OQ}$, And then find the relationship between $\overrightarrow{OP},\text{ }\overrightarrow{OQ}\text{ and }\overrightarrow{PQ}$ using the triangle law of addition. Then, with the help of this relation, we can easily find the distance vector $\overrightarrow{PQ}$.

Complete step by step answer:
Let us assume a point A such that the coordinates of A in a three dimensional coordinate system is (a, b, c). We know that the origin is O (0, 0, 0). We can easily say that the vector starting from the origin O and terminating at point A is called the position vector of point A.
We all know very well that $\hat{i}$ is the unit vector in the direction of positive X-axis, $\hat{j}$ is the unit vector along the direction of positive Y-axis and $\hat{k}$ is the unit vector along the direction of positive Z-axis.
So, we can write the position vector of point A mathematically as
$\overrightarrow{OA}=a\hat{i}+b\hat{j}+c\hat{k}$.
Similarly, let us assume another point B (d, e, f). The position vector of point B can be written as
$\overrightarrow{OB}=d\hat{i}+e\hat{j}+f\hat{k}$
We have shown the vectors $\overrightarrow{OA},\text{ }\overrightarrow{OB}\text{ and }\overrightarrow{AB}$ in the figure below.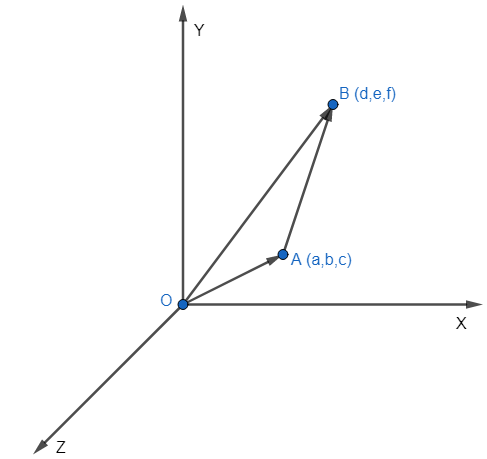
We know that by the triangle law of addition of vectors, we can write
$\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}$.
Thus, we can write
$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$
where, $\overrightarrow{AB}$ is the vector with A as starting point and B as terminating point.
Here, in this question, the starting point of this vector is P (2, -3, 5) and terminal point is Q (3, -4, 7). So, we need to replace A with P and B with Q.
So, by using the above concept, we can write
$\begin{aligned} & \overrightarrow{OP}=2\hat{i}-3\hat{j}+5\hat{k} \\\ & \overrightarrow{OQ}=3\hat{i}-4\hat{j}+7\hat{k} \\\ \end{aligned}$
And, using the triangle law of addition, we can write
$\overrightarrow{OP}+\overrightarrow{PQ}=\overrightarrow{OQ}$
Or, we can write
$\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}$
Thus, we get
$\overrightarrow{PQ}=\left( 3\hat{i}-4\hat{j}+7\hat{k} \right)-\left( 2\hat{i}-3\hat{j}+5\hat{k} \right)$
Hence, we now have $\overrightarrow{PQ}=\hat{i}-\hat{j}+2\hat{k}$.
So, the correct answer is “Option a”.

Note: We know that the subtraction of two vectors $\overrightarrow{OB}=d\hat{i}+e\hat{j}+f\hat{k}$ and $\overrightarrow{OA}=a\hat{i}+b\hat{j}+c\hat{k}$ is written as $\overrightarrow{AB}=\left( d-a \right)\hat{i}+\left( e-b \right)\hat{j}+\left( f-c \right)\hat{k}$. WE must remember that the two vectors $\overrightarrow{OA},\text{ and }\overrightarrow{OB}$ as shown in the figure, are called position vectors, and the vector $\overrightarrow{AB}$ is called the distance vector.