Question

The vector $\overrightarrow {OA}$, where $O$ is the origin is given by $\overrightarrow {OA} = 2\widehat i + 2\widehat j$. Now it is rotated by $45^\circ$ anticlockwise about $O$. What will be the new vector?
1.$2\sqrt 2 \widehat j$
2.$2\widehat j$
3.$2\widehat i$
4.$2\sqrt 2 \widehat i$

Answer 1

We will first find the angle that $\overrightarrow {OA}$ makes with the $x -$ axis. Then we will rotate $\overrightarrow {OA}$ anticlockwise about the origin and find the new angle. Finally, we will find the $x$ and $y$ components of the new vector and represent it in the form of a vector.

Formula used:
If $O$ is the origin and $A$ is any point such that the vector $\overrightarrow {OA} = x\widehat i + y\widehat j$, then $\left| {\overrightarrow {OA} } \right| = \sqrt {{x^2} + {y^2}}$.
If $\theta$ is the angle that $\overrightarrow {OA}$ makes with the $x -$ axis, then $\tan \theta = \dfrac{y}{x}$.

Complete step-by-step answer:
It is given that $\overrightarrow {OA} = 2\widehat i + 2\widehat j$, where $\widehat i{\text{ and }}\widehat j$ are unit vectors along $x{\text{ and }}y$ respectively.

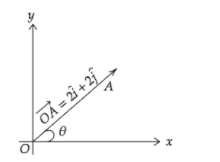
Here, $x -$ component of $\overrightarrow {OA}$ is $2$ and $y -$ component of $\overrightarrow {OA}$ is $2$.
Let $\theta$ be the angle that $\overrightarrow {OA}$ makes with the $x -$ axis. Then,
\tan \theta = \dfrac{y}{x} \\\ \Rightarrow \tan \theta = \dfrac{2}{2} = 1 \\\
We know that $\tan 45^\circ = 1$, so substituting this in above equation, we get
$\Rightarrow \tan \theta = \tan 45^\circ$
$\Rightarrow \theta = 45^\circ$
Now, let us rotate $\overrightarrow {OA}$ anticlockwise about the origin by $45^\circ$. Let $\alpha$ be the angle that the new vector makes with the $x -$axis.
We observe that
$\alpha = \theta + 45^\circ$
Substituting $\theta = 45^\circ$ in the above equation, we get
\Rightarrow \alpha = 45^\circ + 45^\circ \\\ \Rightarrow \alpha = 90^\circ \\\
Let us now find the components of the new vector.
Substituting $x = y = 2$ in the formula $\left| {\overrightarrow {OA} } \right| = \sqrt {{x^2} + {y^2}}$, we get
$\left| {\overrightarrow {OA} } \right| = \sqrt {{2^2} + {2^2}}$
Applying the exponent on the terms, we get
$\Rightarrow \left| {\overrightarrow {OA} } \right| = \sqrt 8 = 2\sqrt 2$
The $x -$component of $\overrightarrow {OA} = \left| {\overrightarrow {OA} } \right|\cos \alpha \widehat i$
Substituting $\left| {\overrightarrow {OA} } \right| = 2\sqrt 2$ in the above equation, we get
$\overrightarrow {OA} = 2\sqrt 2 \cos 90^\circ \widehat i$
Now substituting $\cos 90^\circ = 0$ in the above equation, we get
$\Rightarrow \overrightarrow {OA} = 0\widehat i$
The $y -$component of $\overrightarrow {OA}$ $= \left| {\overrightarrow {OA} } \right|\sin \alpha {\text{ }}\widehat j$
Substituting $\left| {\overrightarrow {OA} } \right| = 2\sqrt 2$ in the above equation, we get
$\overrightarrow {OA} = 2\sqrt 2 \sin 90^\circ \widehat j$
Now substituting $\sin 90^\circ = 1$ in the above equation, we get
$\Rightarrow \overrightarrow {OA} = 2\sqrt 2 \widehat j$
Hence, the new vector $\overrightarrow {OA} = 0\widehat i + 2\sqrt 2 \widehat j = 2\sqrt 2 \widehat j$.
Thus, option (1) is the correct option .

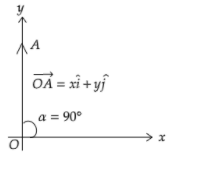
Note: If a vector $\overrightarrow {OA}$ makes an angle $\theta$ with the $x -$axis, then the $x{\text{ and }}y$ components of $\overrightarrow {OA}$ are given as $\left| {\overrightarrow {OA} } \right|\cos \theta$ and $\left| {\overrightarrow {OA} } \right|\sin \theta$ with unit vectors $\widehat i{\text{ and }}\widehat j$ respectively. We have selected the position of $\overrightarrow {OA}$ in the first quadrant since both $x{\text{ and }}y$ components are positive. We can also approach the above problem as follows: After rotating the vector by $45^\circ$, the new vector lies on the $y -$axis. In this case, the $x -$component of the new vector will be zero, which is what we obtained.