Question
Question: The variation of voltage (V) time (t) is shown in the graph. The RMS value of voltage is  time (t) is shown in the graph. The RMS value of voltage is
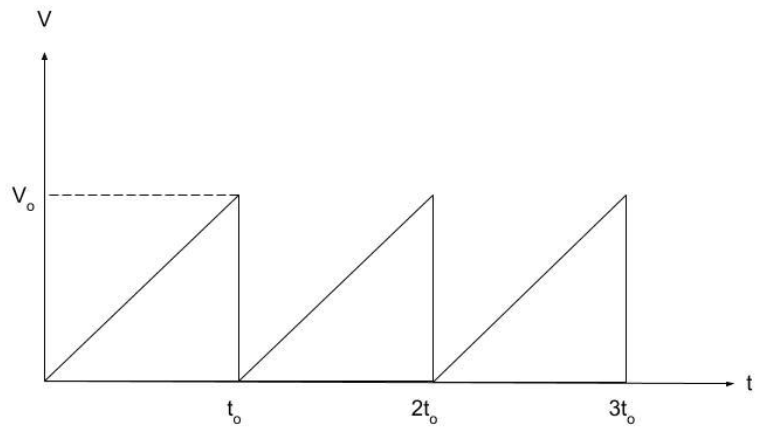
Solution
To solve this question we must know about the concept of RMS value of the voltage and why its necessity was felt. We very well know that the value of voltage in direct current always remains constant. But, in the case of alternating current, the value of voltage continuously keeps on changing. Hence we need one fixed value of voltage for the sake of simplifying our calculations, hence RMS values are used.
Complete answer:
We know that the root mean square value of the voltage is the square root of the time average of the voltage squared. Mathematically, we can write it in the form of the following expression
VRMS=T0∫T[V(t)]2dt…….(1)
Where V(t) represents voltage as the function of time t and T represents the time period over which the RMS value is to be calculated.
From, the graph we can say that V(t) for 0 to t is given by,
V(t)=mt
From the graph the slope m is given by, m=toVo putting this value in the above equation we get,
V(t)=toVot……(2)
Using equations (1) & (2) we can calculate the RMS value for voltage between time 0 to to, by putting T = to in equation (1).
⇒VRMS=to0∫to(toVot)2dt
⇒VRMS=to(toVo)20∫tot2dt
⇒VRMS=to(toVo)2[3t3]0to
⇒VRMS=(to3Vo2)[3to3]
∴VRMS=3Vo
Hence, for the given waveform the root mean square value of the voltage for the time period 0 to to is 3Vo
Hence, the correct answer is option (B).
Note: Usually a sinusoidal waveform is used for an alternating current because the rotating motion (steady rotation) of the magnetic rotor leads to a sinusoidal variation of generated voltage in the winding of the stator and consequently in any circuit which is connected to the output. For a sine wave the root mean square value is taken to be 0.707 times its peak value (VRMS=2Vo=0.707Vo) , where Vo is the peak value of the voltage.
