Question

The variation of square of the speed of sound $\left( {{V}^{2}} \right)$ and absolute temperature of a gas $\left( T \right)$ is shown correctly by,
A.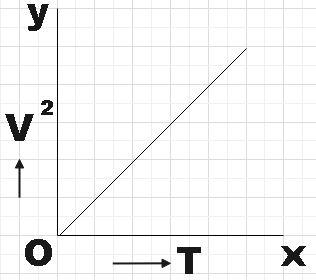

B.

C.

D.

Answer 1

We know that in order to find the correct plot showing the variation of ${{V}^{2}}$with temperature, we should know how they are related to each other. You could either recall such a relation directly or you could derive it from some known relation and doing necessary substitutions. From the relation so found, you could easily answer the question.

Formula used:
Speed of sound,
${{V}_{s}}=\sqrt{\dfrac{\gamma RT}{M}}$

Complete Step by step solution:
In the question, we are asked to find which among the given options correctly represents the variation of the square of the speed of sound with absolute temperature. In order for us to answer this question, we should firstly find out the relation between these two quantities.
You may recall that the velocity of sound is given by,
${{V}_{s}}=\sqrt{\dfrac{\gamma P}{\rho }}$ ……………………………………………… (1)
Where,$\gamma$ is the adiabatic index, P is the pressure of the gas and $\rho$ is the density.

But we need to find a relation in terms of the absolute temperature of the gas. For that, we could recall ideal gas equation given by,
$PV=nRT$
$\Rightarrow P=\dfrac{RT}{V}=\dfrac{RT}{\dfrac{M}{\rho }}$
$\therefore \rho =\dfrac{PM}{RT}$ ……………………………………………….. (2)

Substituting (2) in (1), we get,
${{V}_{s}}=\sqrt{\dfrac{\gamma RT}{M}}$ ……………………………………………. (3)
Where, M is the molar mass of the gas, R is the universal gas constant and T is the absolute temperature.

Squaring equation (3) on both sides we get,
${{V}_{s}}^{2}=\dfrac{\gamma R}{M}T$

But we know that $\gamma$ and M for a particular gas would be constant and R is a universal constant, so,
${{V}_{s}}^{2}=kT$ ………………………………………………….. (4)
Where, k is a constant.

Now, you may recall that equation of a straight line is given by,
$y=mx+c$

Comparing with (4) we see that,
$y={{V}_{s}}^{2}$
$m=k$
$x=T$
$c=0$

So, we could conclude that equation (4) represents a straight line with intercept zero (passes through origin) and as $k=\dfrac{\gamma R}{M}$ is the slope here it would be a positive slope. Therefore, we found that, the variation of square of the speed of sound $\left( {{V}^{2}} \right)$ and absolute temperature of a gas $\left( T \right)$ is shown correctly by,

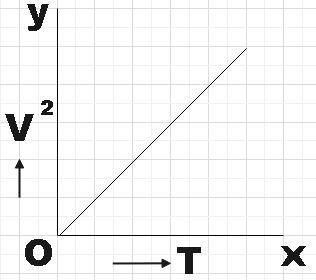
Hence, option A is found to be the correct answer.

Note:
We could define the speed of sound as the distance travelled by a sound wave per unit time. This speed has negligible dependence on frequency and pressure in ordinary air thus slightly deviating from the ideal behavior. In the case of ideal gas as the medium of propagation, the speed only depends on composition and temperature.